Le projectile

Série d’exercices de physique 3ème année Maths Sc.Exp et Tech
1
Théorème de l’énergie cinétique(rotation) - Mouvement d’un projectile
Exercice 1
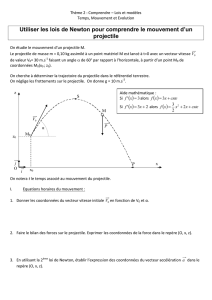
On considère le système (S) représenté par le schéma ci-
contre. Il comprend :
- Une tige (T) homogène de masse MT = 400g et de
longueur L=60 cm solidaire d’un cylindre (C) de rayon
r=0,2 m et de masse M = 200g, mobile sans
frottement autour d’un axe horizontal () passant par
son centre.
- Deux masselottes A et B assimilables à des points
matériels de même masse m=100 fixées sur la tige à
égale distance d =20 cm de .
Un fil inextensible de masse négligeable enroulé sur la poulie, à son extrémité libre est appliquée une
force F constante. Après avoir effectué n=50 tours, le système acquiert une vitesse angulaire de 300
trs.min-1.
1- Calculer le moment d’inertie du cylindre par rapport à l’axe .
2- Calculer le moment d’inertie de la tige (T) par rapport à l’axe .
3- Déduire le moment d’inertie J du système (S).
4- En appliquant le théorème de l’énergie cinétique, Déterminer l’expression de la force F en
fonction de J , ’ (vitesse angulaire) et n. Calculer la valeur de F.
5- Après avoir effectué n=50 tours, la force F est supprimée :
a- Quel est le mouvement ultérieur du système ?
b- Pour arrêter le système, on applique un couple de forces constantes (F1 ; F2) sur le
cylindre
 Représenter le couple de forces.
 Calculer le moment de ce couple sachant que le système s’arrête après 10 tours. Déduire
la valeur de l’une des forces F1 ou F2
Exercice 2 :
Lors d’un match de basket, pour marquer un
panier, il faut que le ballon passe dans un cercle
métallique situé dans un plan horizontal, à 3m du
sol. On assimile le ballon à un point matériel qui
doit passer exactement au centre C du cercle
métallique. xOy est un plan vertical contenant le
point C ; xOz est le plan du sol supposé
horizontal.
1/ D’un point A de Oy situé à 2m du sol, un
basketteur, sans adversaire, lance le ballon, avec
une vitesse
0
V
contenue dans le plan xOy et dont
la direction fait un angle =45o avec un plan
horizontal.
On négligera l’action de l’air et on prendra g=10m.s-2.
a- Montrer que la trajectoire est plane.
b- Etablir l’équation de cette trajectoire dans le système d’axes indiqué, en fonction de la valeur V0
de la vitesse initiale.
c- Quelle doit être la valeur de V0 pour que le panier soit réussi, sachant que les verticales de A et
de C sont distantes de 7,1m ?
d- Quelle est la durée du trajet effectué par le ballon du point A au point C ?
o
z
y
x
A
C
0
V
m
m
d
d
F
(T)
(C)

Série d’exercices de physique 3ème année Maths Sc.Exp et Tech
2
2/ Voulant arrêter le ballon, un adversaire situé à 0,9m du tireur, saute verticalement en levant les
bras. La hauteur atteinte alors par ses mains est de 2,7m au dessus du sol.
 et V0 ayant les mêmes valeurs que précédemment, le panier sera-t-il marqué ?
Exercice N˚2
D’un canon faisant un angle =60˚avec l’horizontal est lancé un projectile a la date t=0 pour attaquer
une cible (un char) se trouvant derrière une
montagne dont le sommet S
a pour coordonnées ( xS=440m ; yS=375m )
dans un repère
,,o i j
.
1/a- Etablir l’équation de la trajectoire du
projectile dans le même repère.
b- Quelle doit être la valeur minimale de la
vitesse
0
V
de lancement pour que le
projectile surmonte le sommet S ?
2/ Etant donné que le projectile est lancé
avec une vitesse V0 = 120ms-1.
a- Quel doit être l’abscisse xC de la cible
pour qu’elle soit touchée par le
projectile?
b- A quelle date sera t-elle touchée?
Exercice 3 :
Un avion de guerre
supersonique est animé d’un mouvement
rectiligne uniforme à la vitesse V0 = 400
m.s-1 vole à une altitude de 2000 m, son
radar a détecté un véhicule de transport de
soldats ennemis supposé ponctuel, immobile au
point A, le pilote a décidé de les attaquer, malgré
l’interdiction de ce fait par la loi de Genève. En
passant par O origine du repère (O,i,j) l’avion a
lâché, à une date prise comme origine de temps,
une bombe qui après quelques secondes a détérioré
complètement le véhicule et a tué tous les soldats.
1- En négligeant la force résistance de l’air et en
appliquant la relation fondamentale de la
dynamique à la bombe déterminer les
composantes selon l’axe (0,x) et selon l’axe (O,y)
de son accélération.
2- Etablir les lois horaires de mouvement de la bombe selon les deux axes.
3- En déduire l’équation de la trajectoire de la bombe relativement au repère (O,i,j).
4- A quelle distance de la verticale passant par O se trouvait le véhicule ? Déterminer la date
d’arrivée de la bombe au véhicule.
5- Où se trouvait l’avion à la date d’arrivée de la bombe au véhicule ?
6- Déterminer les caractéristiques du vecteur vitesse de la bombe lorsqu’elle se trouvait à 1000 m au
dessus du sol.
O
S
Un char
Un canon
y
x
0
V
xS
yS
O
i
j
V0
x
y
2000 m