Portail à battants

840910995
TD MOUVEMENT DE ROTATION
Portail à battants
Un installateur spécialisé dans la pose de systèmes d’ouverture automatique de portails est amené à
s’intéresser aux équations d’ouverture et de fermeture de ses portails en vue d’effectuer la
programmation de leur partie commande.
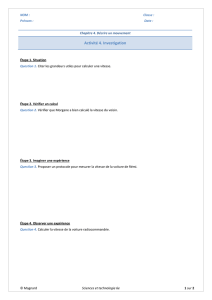
L’extrémité A du battant gauche a un mouvement circulaire dont on donne les équations horaires pour
les différentes phases.
Mouvement d’ouverture :
Phase1 : partant du repos, le battant atteint une
vitesse de rotation de 1,91 tr/min en 1 s.
Phase 2 : le battant tourne à vitesse constante
pendant 6,85 s.
Phase 3 : le battant s’arrête en 1 s.
Mouvement de fermeture :
Phase 4 : partant du repos, le battant atteint une
vitesse de rotation de –1,91 tr/min en 1s.
Phase 5 : le battant tourne à vitesse constante
pendant 6,35 s.
Phase 6 : le battant s’arrête en 2 s.
A- Etude du mouvement d’ouverture.
1- Quelle est la trajectoire du point A?
2- Pour chaque phase, déterminer la nature du mouvement ainsi que les équations horaires.
3- Calculer l’angle d’ouverture f, en degrés, du battant.
4- Calculer, à l’instant t = 5 s , les position, vitesse et accélération angulaires du point A.
En déduire, à cet instant, la valeur :- de la vitesse linéaire v(t=5 s) du point A.
- des accélérations normales et tangentielles du point A.
5- Tracer sur un schéma - le vecteur vitesse V (A  portail / Ro) à t = 5 s.
- le vecteur accélération  (A  portail / Ro) à t = 5 s.
B- Etude du mouvement de fermeture.
1- Pour chaque phase, déterminer la nature du mouvement ainsi que les équations horaires.
3- Vérifier, qu’en fin de fermeture, le portail est bien revenu en position initiale.
C- Graphe des vitesses
Tracer les graphes des vitesses et des accélérations angulaires pour toutes les phases.
Echelle des temps conseillée: 1 cm / 1 s.
A (0 s.)
A (t)
A (8,85 s.)
 (t)
xo
yo
L = 1,5 m
O