Un rectangle est un parallélogramme particulier

582698411 1
Parallélogrammes particuliers
I Rectangle
1) définition
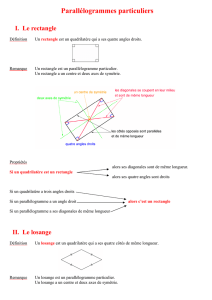
Un rectangle est un quadrilatère qui a ses quatre angles droits
Remarque :
On a (AB)  (BC) et (DC)  (BC)
Or si deux droites sont perpendiculaires à une même
troisième droite, alors elles sont perpendiculaires entre
elles ;
Donc (AB) // (DC)
De même (BC) // (AD), on peut donc affirmer :
Un rectangle est un parallélogramme particulier
A B
D C
2) centre et axes de symétrie
Un rectangle est un parallélogramme particulier, le point d’intersection des diagonales est donc un centre
de symétrie.
Un rectangle admet un centre de symétrie
Un rectangle admet deux axes de symétrie : les médiatrices de deux côtés consécutifs
3) propriétés
a) des côtés
Un rectangle étant un parallélogramme particulier :
Dans un rectangle les côtés opposés sont parallèles et isométriques
D’après la définition du rectangle, on sait également que :
Dans un rectangle deux côtés consécutifs sont perpendiculaires
b) des diagonales
un rectangle étant un parallélogramme particulier :
Dans un rectangle les diagonales se coupent en leur milieu
()

582698411 2
on considère un rectangle ABCD et
() la médiatrice de [AB].
Dans la symétrie par rapport à () :
B est le symétrique de A
D est le symétrique de C
Le symétrique de [AD] est donc [BC], or une symétrie axiale conserve les distances on peut donc conclure
que AD = BC
Dans un rectangle les diagonales sont isométriques
4) Réciproquement
a) avec les angles
On considère un quadrilatère EFGH ayant trois
angles droits.
On sait que : (EF)  (FG), (FG)  (GH) et
(GH)  (HE)
Démontrons que (HE)  (EF)
Ce que l’on sait
Propriété, théorème, définition utilisé
Ce que l’on peut conclure
(EF)  (FG)
(GH)  (FG)
Si deux droites sont perpendiculaires à une même
troisième droite, alors elles sont parallèles entre
elles.
(EF) // (GH)
(EF) // (GH)
(GH)  (HE)
Si deux droites sont parallèles, toute
perpendiculaire à l’une est perpendiculaire à l’autre
(EF)  (HE)
On peut donc écrire le théorème suivant
Si un quadrilatère a trois angles droits, alors ce quadrilatère est un rectangle
De même on admettra que :
Si un parallélogramme a un angle droit, alors ce parallélogramme est un rectangle
b) avec les diagonales
On admettra les deux théorèmes suivants :
Si les diagonales d’un quadrilatère se coupent en leur milieu et sont isométriques, alors ce quadrilatère est
un rectangle
Si les diagonales d’un parallélogramme sont isométriques, alors ce parallélogramme est un rectangle
A
B
C
D
E
F
G
H

582698411 3
II Losange
1) définition
Un losange est un quadrilatère dont les (quatre) côtés sont isométriques
On admettra qu’un losange est un parallélogramme particulier
2) centre et axes de symétries
Un losange est un parallélogramme particulier, le point d’intersection des diagonales est donc un centre de
symétrie.
Un losange admet un centre de symétrie
On considère un losange ABCD
On a AD = CD et AB= CB, et B distinct de D.
Si un point est équidistant des extrémités d’un segment, alors
ce point appartient à la médiatrice de ce segment
donc (BD) est la médiatrice de [AC].
C est le symétrique de A par rapport (BD)
B et D sont leurs propres symétriques par rapport à (BD)
(BD) est donc un axe de symétrie.
De même (AC) est un axe de symétrie
Un losange admet deux axes de symétrie : ses diagonales
3) propriétés
a) des côtés
D’après la définition du losange
Dans un losange les côtés sont isométriques
Un losange étant un parallélogramme particulier
Dans un losange les côtés opposés sont parallèles
b) des diagonales
Un losange étant un parallélogramme particulier
I
J
K
L
A
B
C
D

582698411 4
Dans un losange les diagonales se coupent en leur milieu
On considère un losange ABCD, on a vu que (BD) était la médiatrice de [AC], on a donc (BD)  (AC)
Dans un losange les diagonales sont perpendiculaires
4) réciproquement
a) avec les côtés
D’après la définition du losange
Si les côtés d’un quadrilatère sont isométriques, alors ce quadrilatère est un losange
On admettra que :
Si un parallélogramme a deux côtés consécutifs isométriques, alors ce parallélogramme est un losange.
b) avec les diagonales
Si les diagonales d’un quadrilatère sont perpendiculaires et se coupent en leur milieu, alors ce quadrilatère
est un losange
(démonstration utilisant propriété des médiatrices)
Si les diagonales d’un parallélogramme sont perpendiculaires, alors ce parallélogramme est un losange
III Carré
Un carré est un quadrilatère qui a ses (quatre) angles droits et ses (quatre) côtés isométriques.
Un carré est donc à la fois un rectangle particulier et un losange particulier.
Il possède donc toutes les propriétés du rectangle et du losange.
Un carré admet un centre de symétrie et quatre axes de symétrie.
On a également les théorèmes suivants :
Si un quadrilatère a trois angles droits et deux côtés consécutifs isométriques, alors ce quadrilatère est un
carré
Si les diagonales d’un quadrilatère sont perpendiculaires, isométriques et se coupent en leur milieu, alors ce
quadrilatère est un carré