DM2-ND-corrigé

Nom : Classe :
Prénom : Groupe :
Devoir maison 2 (1h)
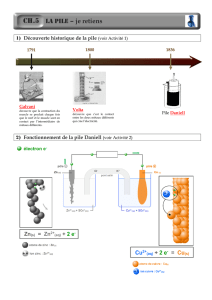
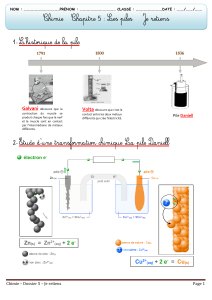
Exercice 1 : La face cachée de la pile (/8)
Question 1 : Les parties correspondant à la pile sont la solution de sulfate
de cuivre et les lames de cuivre et de zinc.
Question 2 : Pourquoi, lorsque la pile fonctionne :
a. Les ion cuivre II responsables de la couleur bleue de la solution
réagissent pour former des atomes de cuivre. Ils disparaissent donc de la
solution au cours du fonctionnement de la pile, faisant perdre sa couleur à la
solution.
b. Les atomes de zinc sont eux aussi consommés, la lame de zinc est
donc rongée.
Question 3 : Cet ensemble possède de l’énergie chimique.
Question 4 : L’énergie chimique est convertie en énergie électrique.
Question 5 : Une pile s’use car les réactifs sont consommés. Une fois
qu’ils sont complètement consommés, la réaction responsable de l’énergie
électrique ne se fait plus. La pile est usée.
Question 6 : Le courant électrique dans les fils métalliques à l’extérieur de la pile est dû à un déplacement d’électrons libres.
Question 7 : Le courant électrique dans la solution est dû à un déplacement d’ions.
Question 8 : Les ions positifs qui se déplacent dans la solution lorsque la pile fonctionne sont les ions cuivre II (Cu 2+)
Question 9 : (voir schéma)
Exercice 2 : En Montand, à bicyclette (/5) :
Question 1 : Puisque qu'un tour correspond à une période et que la
fréquence est le nombre de périodes par secondes, la fréquence du signal
généré par l'alternateur correspond au nombre de tours par seconde. On
a donc f = 30 / 60= 0,5 Hz. La fréquence du signal vaut f = 0,5 Hz.
Question 2 : La période est liée à la fréquence par la relation : T= 1 / f.
On a donc : T = 1 / 0,5 = 2 s. La période du signal généré par
l'alternateur est T = 2 s.
Question 3 : Si le cycliste fait deux fois plus de tours par minute, la fréquence est multipliée par 2. Or T=1/f : la période est
inversement proportionnelle à la fréquence et sera donc divisée par 2. Donc T = 2/ 2 = 1 s. Si le cycliste roule deux fois plus
vite, la période devient T=1 s.
Question 4 : Un motif élémentaire correspond à la période T = 1 s. D'après le schéma, la tension s'annule pour la première
fois à l'instant t = T / 2 = 0,5 s. Les autres instants d'annulation de la tension s'obtiennent en respectant la périodicité du
signal. Voir schéma.
Question 5 : Le schéma représente deux motifs élémentaires, donc deux périodes. Chaque période correspond à un seul tour
de pédales. Le schéma correspond donc à deux tours de pédales.
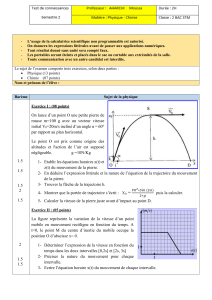
Exercice 3 : Etude de signal (/5) :
Question 1 Les valeurs du tableau permettent d’affirmer que la tension est variable et alternative.
Question 2 : Echelle verticale (1cm -> 0,5 V)
Question 3 : Cette tension est périodique
Question 4 : Sur ce graphe, il y a 2 périodes.
Question 5 : Par lecture graphique, U1 = 3,3 V et
U2 = - 5 V
Question 6 : 1 période vaut 80 s. On cherche
combien de périodes dans 2 minutes soient 120 s.
120 / 80 = 1,5 périodes. La tension aura atteint 3
fois les sommets (deux maxima et un minimum), la
lampe sera éclairée 3 fois à son maximum.