EXERCICE III Détection de Métaux (4 points)

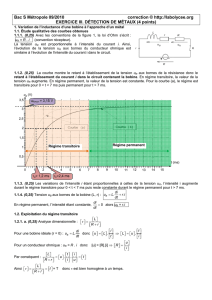
Bac S Métropole 09/2010
correction © http://labolycee.org
EXERCICE III. DÉTECTION DE MÉTAUX (4 points)
1. Variation de l’inductance d’une bobine à l’approche d’un métal
1.1. Étude qualitative des courbes obtenues
1.1.1. (0,25) Avec les conventions de la figure 1, la loi d’Ohm s’écrit :
uR = R . i.. (convention récepteur).
La tension uR est proportionnelle à l’intensité du courant i. Ainsi,
l’évolution de la tension uR aux bornes du conducteur ohmique est
similaire à l’évolution de l’intensité du courant i dans le circuit.
L
r
R
uB
uR
i
K
-
+
E
1.1.2. (0,25) La courbe montre le retard à l’établissement de la tension uR aux bornes de la résistance donc le
retard à l’établissement du courant i dans le circuit contenant la bobine. En régime transitoire, la valeur de la
tension uR augmente. En régime permanent, la valeur de la tension est constante. Pour la courbe (a), le régime est
transitoire pour 0 < t < 7 ms puis permanent pour t > 7 ms.
uR (V)
3,5
uRmax = 3,15 V
3
2,5
Courbe ( b)
Courbe (a )
2
1,5
Régime permanent
Régime transitoire
1
0,5
t (ms)
0
1
2
a= 1,2 ms
3
4
5
6
7
8
9
10
11
12
13
14
15
b=2,4 ms
1.1.3. (0,25) Les variations de l’intensité i étant proportionnelles à celles de la tension uR, l’intensité i augmente
durant le régime transitoire pour 0 < t < 7 ms puis reste constante durant le régime permanent pour t > 7 ms.
di
1.1.4. (0,25) Tension uB aux bornes de la bobine (L, r) : uB  L.  r .i
dt
di
 0 alors uB = r.i…
En régime permanent, l’intensité étant constante,
dt
1.2. Exploitation du régime transitoire
L 
1.2.1. a. (0,25) Analyse dimensionnelle :     
R  r 
Pour une bobine idéale (r = 0) : uB  L.
i 
t 
di
donc u   L  .    L   u  .  
dt
t 
i 
Pour un conducteur ohmique : uR = R . i donc
Par conséquent :
u 
[u] = [R].[i]  R    
i 
L 
t   i 
 u  .   .    t 
R  r 
i  u 
L 
Ainsi       t  = T
R  r 
donc  est bien homogène à un temps.
1.2.1.b. (0,25) Pour t = , la tension uR est égale à 63% de sa valeur maximale.
Or uRmax = 3,15 V donc : 0,63 × 3,15  0,63 × 3,2 = (0,63 ×3 + 0,63×0,2) = 1,89 + 0,126 = 2,016 V  2,0 V.
On trace la droite horizontale U = 2,0 V. Cette droite coupe les courbes (a) et (b) en des points dont les abscisses
respectives sont les constantes de temps  a et  b . On lit graphiquement : a = 1,2 ms et b = 2,4 ms.
1.2.2. (0,25) Comme

Ainsi : La =  a . (R+r)
Lb =  b . (R+r)
Donc
L
alors L =  . (R +r).
Rr
(bobine seule)
(bobine proche d’un morceau de fer)
La  a
 < 1 car a < b d’où Lb > La. On vérifie bien l’information donnée dans le texte « l’inductance
Lb  b
augmente si on approche de la bobine un objet en fer ».
2. L’oscillateur
2.1. (0,25) Avec les conventions de la figure 3, uL  L.
2.2. (0,25) On a i 
uL
di
.
dt
d (C.uC )
du
dq
 C. C
et q = C.uC donc i 
dt
dt
dt
L
car C est
i
uC
q
constante.
2.3. (0,25) La loi d’additivité des tensions donne : uC + uL = 0
d  du 
di
Soit uC + L. =0

uC + L  C. C  = 0
dt 
dt 
dt
C
Figure 3. L’oscillateur
d 2uC
=0
dt 2
2.4. (0,25) En divisant chaque terme par LC, l’équation différentielle précédente peut se mettre sous la forme :
d 2uC
1

.uC  0
2
L
.C
dt
(0,25) 
uC + L.C.
En comparant les deux équations différentielles :
d 2uC
d 2uC 4 2
1
4 2
1
avec
on
peut
écrire
:
soit T02  4 2 .LC

.
u

0

.
u

0

.
C
C
2
2
2
2
L.C
L.C
dt
dt
T0
T0
.
Soit finalement, en ne gardant que la solution positive : T0  2 LC
uC (V)
2.5. (0,25) Graphiquement,
T0 = 50 µs = 5,0 × 105 s
T0
T0
2.6. (0,25) Comme T02  4 2 .L.C
4
alors C 
2
t (µs)
0
20
40
60
80
100
-2
T02
4 2 .L
5,0  10 
5
C
2
4  10  20.103
25  1010
C
 3,1 109 F
8,0  101
soit C = 3,1 nF.
-4
3. Recherche de métaux
3.1. (0,25) La fréquence propre de l’oscillateur est : f 0 
1
. Si on approche de la bobine un objet en or, la
2 LC
valeur de l’inductance L de la bobine diminue. Comme C est constante, alors la fréquence propre de l’oscillateur
augmente.
3.2. (0,25) En l’absence d’objet métallique à proximité de la bobine, la fréquence propre de l’oscillateur est 20 kHz.
Si Léo et Julie détectent un signal de fréquence 15 kHz, alors la fréquence propre a diminué donc l’inductance de la
bobine a augmenté. Malheureusement, ils n’ont pas trouvé de l’or mais plus surement un objet d’un autre métal.