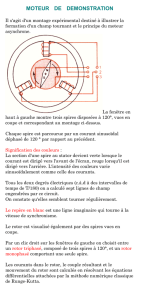
rotor_contraintes

Définition des symboles utilisés.
= flux sous un pôle.
Be= induction max. au niveau de l’entrefer.
Ac =charge linéique (au niveau de l’alésage du stator).
L= longueur du stator.
D= diamètre d’alésage du stator.
Dr= diamètre extérieur du rotor.
e= entrefer.
p= nombre de paire de pôles de la roue polaire.
kb= coefficient de bobinage.
Nc= nombre de conducteurs en série par phase.
Les fuites magnétiques seront négligées.
La force électromotrice par phase peut s’écrire :
2
E
.kb.Nc.f.
On peut donner l’expression de  : flux sous un pôle
pDLBe
SBe .. .
La puissance apparente de l’alternateur (fonctionnant à fréquence constante) est :
2
.3..3  IES
.kb.Nc.f.
pBeDL ..
.I
L’expression de la charge linéique est donnée par la formule suivante :
D
IeNe
Ac ..
avec Ie = courant dans une encoche =
a
I
nce 2 .
Ne = nombre total d’encoches au stator.
nce= nombre de conducteurs par encoche.
nce
Nca
Ne .2.3
d’ou
DINc
Ac ...3
et donc
Nc
DAc
I.3 ..
soit Sn = 3.
2
.kb.Nc.f.
pBeDL ..
.
Nc
DAc.3 ..
=
2
²
.kb.f.L.D².Be.
p
Ac
Sn = K.L.D².Be.Ac avec K=
2
²
.
p
f
.kb
CONTRAINTES MECANIQUES SUR UN ROTOR DE
TURBO-ALTERNATEUR

Application numérique: Etude d’un turboalternateur de 1485 MW.
Puissance apparente Sn=
6
10.1650
VA.
Vitesse de rotation 1500 tr/min.
Tension nominale 20 kV.
Fréquence 50 Hz.
Intensité nominale 48 kA.
Masse du rotor 240 tonnes, masse du stator 505 tonnes.
Couplage étoile.
Entrefer e= 9,5 cm.
Coefficient de bobinage kb = 0,913.
Nombre de conducteurs en série par phase Nc=14.
Charge linéique Ac= 300 000 A/m.
Induction maximale Be=0,96 T.
Calcul du diamètre D du rotor:
AcINc
D...3
=
300000. 48000.14.3
= 2,13 m
Après avoir calculé la valeur de
2.2
913,0.50².
K
= 159,2
L’expression de Sn permet de trouver la longueur L du rotor:
AcBeDK Sn
L.²..
=
300000.96,0².13,2.2,159 10.1650 6
= 7,93 m
A la périphérie du rotor, de rayon R, la vitesse tangeantielle est:
smR
n
Rv /16706,1.
30
1500.
.
30
.
.
Rotor du turboalternateur.
A la périphérie du rotor, l’accélération centrifuge est, à la vitesse n
2
. Ran 
soit
2
30
.
. n Ran
= 1,06.157² = 26154 m/s²

Cette valeur représente approximativement 2660 fois l’accélération de la pesanteur !
La force centrifuge vaut alors :
anMF .
= 240000.26154 =6,28.109 N
Le moment d’inertie du rotor vaut :
²..
2
1RMJ 
=
.²06,1.10.240
2
13
= 135.103 m².kg
Ce chiffre laisse imaginer les dimensions données à la pièce !
L’énergie cinétique correspondante vaut alors :
2
..
2
1
JW 
=
MJ.1660²157.10.135.
2
13
Prenons un train roulant à 200 km/h, soit 55,6 m/s et calculons quelle devrait être sa masse
pour avoir la même énergie cinétique.
1660.106 =
3090..
2
1M
soit M =
kg
3
610.1070
3090
10.3320 
= 1070 tonnes.
Cela correspond à l’énergie d’un train de 1070 tonnes lancé à 200 km/h !
Pascal Dereumaux
Lycée P.G de Gennes
Quartier St Christophe
04000 Digne les bains
[email protected]