Les transformations du plan

Les transformations du plan
 Arbre des transformations
1) Définition
Une isométrie est une transformation qui conserve la forme et la taille de la
figure.
Une isométrie peut être décrite par un mouvement : déplacer ou retourner.
Dans les déplacements, on trouve les translations, les symétries centrales et les
rotations.
Dans les retournements, on trouve les symétries orthogonales.
2) Arbre des transformations
Symétrie centrale
Rotation
Translation
Symétrie orthogonale
TRANSFORMER
CONSERVER LA FORME
DÉFORMER
CONSERVER LES MESURES
AGRANDIR / RÉDUIRE
DÉPLACER
RETOURNER
GLISSER
TOURNER
TOURNER D’UN DEMI-TOUR

 Caractéristiques des transformations
1) Translation
Définition
L’élément caractéristique d’une translation est le vecteur, symbolisé par une
flèche, selon lequel on effectue un glissement.
Exemple
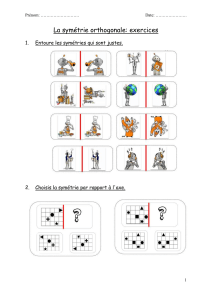
2) Symétrie orthogonale
Définition
L’élément caractéristique d’une symétrie orthogonale est la droite autour de
laquelle on effectue un retournement, on l’appelle l’axe de la symétrie
orthogonale.
Exemple
3) Symétrie Centrale
Définition
L’élément caractéristique d’une symétrie centrale est le point autour duquel on
effectue un demi-tour, on l’appelle le centre de la symétrie centrale.

Exemple
C
 Construction aux instruments
Convention
On désigne souvent un point d’une figure par une lettre majuscule (A, B, X, ….) et son
image par une transformation par la même majuscule à laquelle on ajoute un « ‘ »
(A’, B’, X’, …..). Cela se lit A « prime » est l’image de A, B « prime » est l’image de B …
1) Symétrie orthogonale
Construction de l’image d’un point X par une symétrie orthogonale d’axe a.
Définition
X’ est l’image de X par la symétrie orthogonale d’axe a si a est la médiatrice de
[𝑋𝑋′].
Méthode
Pour construire l’image d’un polygone, il suffit de construire l’image de ses
sommets puis de relier les images entre elles, dans le même ordre que la figure
de départ.
2) Symétrie centrale
Construction de l’image d’un point X par une symétrie centrale de centre C.
Définition
X’ est l’image de X par la symétrie centrale de centre C si C est le milieu de [𝑋𝑋′].
Méthode

Pour construire l’image d’un polygone, il suffit de construire l’image de ses
sommets puis de relier les images entre elles, dans le même ordre que la figure
de départ
3) Translation
Construction de l’image d’un point X par une translation de vecteur 𝐴𝐵
⃗
⃗
⃗
⃗
⃗
Définition
X’ est l’image de X par le translation de vecteur 𝐴𝐵
⃗
⃗
⃗
⃗
⃗
si XX’ est parallèle à AB,
𝑋𝑋′= 𝐴𝐵 et [𝑋𝑋′ dans le même sens que [𝐴𝐵.
Méthode
Pour construire l’image d’un polygone, il suffit de construire l’image de ses
sommets puis de relier les images entre elles dans le même ordre que al figure de
départ.
 Découverte des invariants
Les isométries conservent :
- l’alignement des points, c’est-à-dire que les images par une isométrie de trois
points alignés, sont trois points alignés ;
- le parallélisme des droites, c’est-à-dire que les images de deux droites parallèles
par une isométrie sont deux droites parallèles ;
- l’amplitude des angles (et donc la perpendicularité des droites), c’est-à-dire que
l’image d’un angle par une isométrie est un angle de la même amplitude ;
- les longueurs des segments, c’est-à-dire que l’image d’un segment par une
isométrie est un segment de même longueur.