Les angles :

Les angles :
Sommaire :
1. Notation
2. Mesurer un angle.
3. Construire un angle
4. Bissectrice d’un angle.
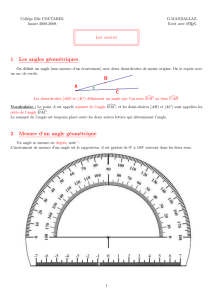
1. Notation :
Envoyer au tableau un élève pour tracer un angle (droit ou quelconque).
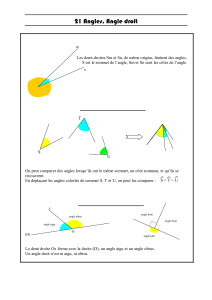
De quoi est composé la figure : deux demi-droites sécantes en un point appelé sommet.
Un angle est formé par deux demi-droites sécantes. Le point d’intersection de ces deux demi-droites est appelé
sommet de l’angle.
Sur une figure, on marque l’angle par un arc de cercle.
Comment nommer un angle : comme pour les droites, demi-droites ; segments... il nous faut un système de
notation pour nommer les angles.
Activité a p 185
Pour nommer un angle, il faut :
- Repérer le sommet
- Placer à gauche et à droite de ce sommet 2 points des deux demi-droites de l’angle.
- Mettre un accent ^ au dessus de ces trois lettres.
Exemple :
A
BC
B est le sommet ; [BC) et [BA) sont les deus demi-droites :
On nomme cet angle l’angle ;CBA ou ;ABC.
Comment nommer un angle ? (présentation .pps)
Deux angles de même mesure sont codés par un même symbole (comme pour deux segments de la même
longueur).
Exo 1 2 p 194 32,33 p 198
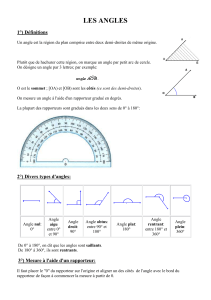
2. Mesurer un angle :
a. Classification des angles :
Variation d’un angle et limite entre obtus et aigu.

Angles droits
Angles aigus
Angles obtus
Angles plats
On vérifie à l’équerre
L’angle fait 90°.
La mesure de l’angle
est inférieure à un
angle droit.
La mesure de l’angle
est supérieure à un
angle droit
Les trois points A, B,
C sont alignés.
Prendre les angles de la page 194 et demandé de les classifier. 34ap198
b. Utilisation du rapporteur
Les faire observer un rapporteur.
Pour mesure un angle on utilise un rapporteur.
- On place le centre du rapporteur sur le sommet de l’angle.
- On aligne le zéro du rapporteur avec un des cotés de l’angle.
- Le nombre correspondant à l’intersection des numérotations avec le deuxième coté de l’angle
correspond à la mesure de l’angle.
Remarque :
 La longueur des « côtés de l’angle » n’ont pas de rapport avec la mesure de l’angle.
 Si les cotés de l’angle sont trop petits, il suffit de les rallonger légèrement au crayon de bois
 On vérifie que si l’angle est aigu, sa mesure est inférieure à 90° et que si l’angle est obtus, il est supérieur à
90°(cela permet de vérifier si on a lu la mesure sur les bonnes graduations.
Voir la rubrique animation pour plus de détails.
3, 5, 6 p 194 34, 36 ,p 198
3. Construire un angle :
Le plus souvent, on donne la mesure d’un angle et c’est à vous de le construire.
Méthode de tracé :
- On place le sommet.
- On trace une demi-droite.
- On positionne le centre du rapporteur sur le sommet et on place un coté du rapporteur sur la demi-
droite.
- On reporte la mesure voulue et on trace la deuxième demi-droite.
Exemple :
Tracer un angle de 115° ; de 43°.
Correction des constructions : 115° et 43°.
A
B
C
A
B
C
A
B
C
AB
C

Remarque : On vérifie également que l’angle tracé correspond bien à un angle aigu si sa mesure est inférieure à
90° et que l’angle est obtus si sa mesure est supérieure à 90°.
Exo 8 p 195
Dans les exercices, on vous demande de tracer des figures complexes mélangeant angles, droites, segments,
longueurs...
Faire le premier triangle 14p195 puis 21 (1) p 196.
15,16,17 p 195 et plus selon temps.
22 p 196
4. Bissectrice d’un angle :
Définition :
La bissectrice d’un angle est une droite qui partage cet angle en deux angles de même mesure.
Méthode de tracé :
Il existe deux façons de tracé une bissectrice :
1. A l’aide du rapporteur :
a. On mesure l’angle.
b. On repère la moitié de cette mesure et on trace la bissectrice.
2. A l’aide du compas :
Voir p 193 sur le schéma
Construction d’une bissectrice.
Exo 12 13 p 195 26 p 196