PREMIER PROBLÈME : GÉOMÉTRIE CAP: Il points

BEP du 30 mai 1997 MATHEMATIQUES SCIENCES (2h00)
Electrotechnique
MATHEMATIQUES
PREMIER PROBLÈME : GÉOMÉTRIE 19 points
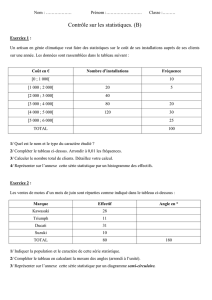
1. La figure 1 représente un carré A1B1C1D1. Ce carré n’est pas
représenté à l’échelle 1. La longueur c1 de son côté est égale à 10
cm.
Calculer, en centimètres-carrés, son aire a1.
2.
a) Placer, sur la figure, les points A2, B2, C2 et D2 tels que :
- A2 est le milieu de [A1B1],
- B2 est le milieu de [B1C1],
- C2 est le milieu de [C1D1],
- D2 est le milieu de [D1A1].
Construire le carré A2B2C2D2.
b) En appliquant le théorème de Pythagore dans le triangle rectangle A1A2D2, calculer, en
centimètres, la longueur c2 du côté du carré A2B2C2D2. Arrondir le résultat à 0,01 cm.
3. Calculer, en centimètres-carrés, l'aire a2 du carré A2B2C2D2.
Arrondir le résultat au centimètre-carré.
4. Placer sur la figure les points A3, B3, C3 et D3 tels que :
- A3 est le milieu de [A2B2],
- B3 est le milieu de [B2C2],
- C3 est le milieu de [C2D2],
- D3 est le milieu de [A2D2].
Construire le carré A3B3C3D3.
5. La longueur du côté du carré A3B3C3D3 est notée c3 et son aire est notée a3.
Calculer c3, sachant que c3 =
Error!
c2 et que c2 = 7,07 cm, arrondir le résultat au centimètre.
6. Calculer, l’aire a3 du carré A3B3C3D3. Arrondir le résultat au centimètre-carré.
7. En reprenant la démarche précédente à partir du carré A3B3C3D3, on obtient un carré
A4B4C4D4 dont la longueur du côté est c4 et dont l’aire est a4. On donne c4 = 3,54 cm et a4 = 12,5 cm2.
a) Recopier ci-dessous les valeurs de a1 ; a2 ; a3 ; a4.
b) Indiquer l’opération qui permet d'obtenir :
a2 à partir de a1, a3 à partir de a2, a4 à partir de a3.
8. Justifier que la suite de nombres a1 ; a2 ; a3 ; a4 est une suite géométrique puis donner la raison de
cette suite.
9. On appelle an l’aire du n-ième carré obtenu par constructions successives. En admettant que la suite
des nombres a1 ; a2 ; a3 ; ……… ; an – 1 ; an est une suite géométrique et en utilisant le formulaire,
exprimer an en fonction de n.
10. Calculer a10 ; arrondir le résultat à 0,01 centimètre-carré.

DEUXIEME PROBLÈME : FONCTIONS NUMERIQUES 21 points
La courbe C1 est la représentation graphique, dans le plan rapporté au repère (O ; I ; J), d’une fonction f de
la variable x, sur l’intervalle [0 ; 8].
x’
I
x
J
y
C1
O
y’

1. Le couple (x ; y) désignant les coordonnées d'un point de C1, compléter, à l’aide du graphique, le
tableau suivant :
x
4
8
y
4
– 5
2. Soit la fonction g de la variable x définie, sur l'intervalle [– 8 ; 6], par g (x) = 1,5 x.
a) cette fonction est :
une fonction affine
une fonction linéaire
Cocher la case correspondant à la bonne réponse.
Justifier le choix fait.
b) la représentation graphique de la fonction g est une droite (D) :
passant par l’origine du repère
ne passant pas par l’origine du repère
Cocher la case correspondant à la bonne réponse.
c) Tracer la droite (D) dans le plan rapporté au repère (O , I , J) de la page précédente.
3. Construire, dans le plan rapporté au repère (O , I , J) de la page précédente, la courbe C2
symétrique de la courbe Cl par rapport à l'axe des ordonnées (y'y).
4. La courbe C, constituée des courbes Cl et C2, est la représentation graphique d'une fonction h de la
variable x, définie sur l'intervalle [– 8 ; 8].
A l'aide de la courbe C, indiquer ci-dessous, quel semble être :
- l’intervalle sur lequel h est croissante :
- l’intervalle sur lequel h est décroissante :
- la valeur maximale de h(x) :
- la valeur de x pour laquelle h(x) est maximal :
5. Cocher, dans le tableau ci-dessous, la case correspondant à l'équation de la courbe C.
y = Error! x2 + 4
y = – Error! x2 + 4
y = – Error! x2 – 4
y = Error! x2 – 4
Justifier le choix fait.
6. Justifier que, sur l’intervalle [– 8 ; 8], la fonction h est une fonction paire.
7. Indiquer à l’aide du graphique ci-dessus, quelles semblent être les abscisses des points
d’intersection de C et de (D).
8. Indiquer pourquoi les abscisses des points d'intersection de C et de (D) doivent vérifier l’égalité :
1,5 x = – 0,25 x2 + 4.

TROISIEME PROBLÈME : CHIMIE 15 points
Description d'une expérience :
Dans un bécher, on place un petit récipient
contenant de l’acide chlorhydrique de formule
brute HCl et un morceau de craie (carbonate de
calcium CaCO3).
Le bécher est fermé hermétiquement à l’aide
d'une membrane élastique (voir schéma
ci-contre).
On incline le bécher afin de renverser l’acide sur la craie. Il se produit un dégagement gazeux de dioxyde
de carbone (CO2) qui gonfle la membrane.
Au fond du bécher, il reste un mélange contenant uniquement de l’eau (H2O) et du chlorure de calcium de
formule brute CaCl2.
1. Écrire le nom des réactifs de cette expérience.
2. Écrire le nom des produits de la réaction chimique décrite.
3. Indiquer, pour chacune des affirmations suivantes, si elle est vraie ou si elle est fausse, en cochant
la case appropriée du tableau.
Affirmation
Vraie
Fausse
La formule du chlorure de calcium indique qu’il y a 2 atomes de
calcium pour 1 atome de chlore.
La formule du chlorure de calcium indique qu’il y a 2 atomes de
chlore pour 1 atome de calcium.
L’ion Cl– provient d'un atome de chlore ayant perdu un électron.
Lors de l’expérience décrite, il se produit un dégagement de
dihydrogène.
4. Après avoir observé le schéma de l’expérience,
a) rappeler :
- la masse du morceau de craie utilisée :
- la masse totale indiquée par la balance au début de l’expérience :
b) prévoir l’indication de la balance à la fin de l’expérience, justifier la réponse.
5. L’équation bilan de la réaction chimique de l’expérience s’écrit :
2 HCl + CaCO3 ; H20 + CaCl2 + CO2
Données :
Volume molaire d'un gaz dans les conditions de l'expérience : 22,4 L/mol
Elément
Symbole chimique
Masse molaire atomique (g/mol)

Azote
N
14
Calcium
Ca
40
Carbone
C
12
Chlore
Cl
35,5
Fer
Fe
56
Hydrogène
H
1
Oxygène
O
16
Sodium
Na
23
Soufre
S
32
Zinc
Zn
65
Calculer le volume de dioxyde de carbone produit à la fin de la réaction.
6. La membrane est percée à la fin de l’expérience. Le dioxyde de carbone s’échappe. Calculer la
masse indiquée alors par la balance.
QUATRIEME PROBLÈME : ELECTRICITE 11 points
Description d’une expérience :
On utilise le dispositif expérimental ci-dessous :
1. Nommer la grandeur physique que l’appareil 1 permet de mesurer, lorsque l'interrupteur K1 est
fermé.
2. Le cadran de cet appareil a été représenté ci-dessous. Le calibre utilisé est 1 ampère.
Indiquer la valeur, en ampères, de la mesure effectuée avec l’appareil 1.
3. La figure ci-dessous représente l’écran de l’oscilloscope.
Le calibre choisi pour les voies 1 et 2 est 5 volts par division. Celui de la base de temps est 2
millisecondes par division.
u1 est la tension d’entrée du transformateur (voie 1) et u2 la tension de sortie (voie 2).