Oscillations électriques libres

Oscillations électriques libres
Dipôle RLC
Exercice 1
Un condensateur est initialement chargé sous une tension E=6,0V puis
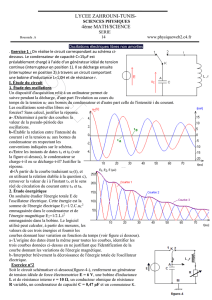
inséré dans le montage suivant.
On considère que la bobine a une résistance interne négligeable. À la
date t=0, on ferme l'interrupteur K.
1. En appliquant la loi d'additivité des tensions, établir une relation [1] entre uL, tension aux
bornes de la bobine et uC, tension aux bornes du condensateur.
2. Exprimer uL en fonction de l'intensité i.
3. Exprimer l'intensité i en fonction de la capacité C et de la tension uC.
4. À l'aide de la relation [1], établir l'équation différentielle à laquelle obéit uC.
5. Une solution de cette équation différentielle est de la forme: uC= a.cos(0t + b).
a. En reportant cette expression dans la relation [1], déterminer l'expression de ω0.
b. À la date t=0, quelle particularité la tension uC présente-t-elle? Quelle est alors sa
valeur?
c. À la date t=0, quelle particularité
l'intensité du courant traversant
le circuit présente-t-elle? En
déduire les constantes b et a.
Quelle est l'expression de uC en
fonction du temps.
Données: C=2200µF; L=1,1H.
Exercice 2
On réalise le montage ci-contre. On prend C=2,0µF. Le condensateur est préalablement chargé
(K en position 1). On bascule K en position 2 et on enregistre les variations de la tension uC aux
bornes du condensateur.On observe l'oscillogramme ci-dessous.
1. Pourquoi parle-t-on d'oscillations libres?
2. Préciser la nature du régime d'oscillation observé.

3. Quelle est la pseudo-période des oscillations observées?
4. En admettant que l'on peut assimiler cette pseudo-période à la période des oscillations non
amorties du circuit LC correspondant, calculer la valeur de l'inductance L de la bobine.
Exercice 3
Un condensateur de capacité C est chargé sous une tension U0=12,0V. On effectue ensuite sa
décharge dans un dipôle série constitué d'une résistance R=30Ω, et d'une bobine d'inductance L et
de résistance r. L'oscillogramme de la tension uR aux bornes de la résistance R est représenté ci-
dessous.
1. Quelle est la valeur de la pseudo-période?
2. Quelle est la relation entre uR et i? Pourquoi la tension uR est-elle négative au début de la
décharge?
3. Quelle est la valeur de l'intensité à l'instant t=0? En déduire la valeur de la tension uL(t=0) aux
bornes de la bobine.
4. Exprimer uL en fonction de L, r, i et di/dt.

5. Mesurer sur la courbe la valeur de di/dt à l'instant t=0. En déduire la valeur de L.
6. En déduire la valeur de C.
Exercice 4
On réalise le circuit correspondant au schéma ci-dessous. Le condensateur de capacité C=15µF
est préalablement chargé à l'aide d'un générateur idéal de tension continue (interrupteur en
position 1). Il se décharge ensuite (interrupteur en position 2) à travers un circuit comportant une
bobine d'inductance L=1,0H et de résistance r.
I. Étude du circuit
1. Étude des oscillations
Un dispositif d'acquisition relié à un ordinateur permet de suivre pendant la décharge, d'une part
l'évolution au cours du temps de la tension uC aux bornes du condensateur et d'autre part celle de
l'intensité i du courant.
a. Les oscillations sont-elles libres ou forcées? Sans calcul, justifier la réponse.
b. Déterminer à partir des courbes la valeur de la pseudo-période des oscillations.
c. Établir la relation entre l'intensité du courant i et la tension uC aux bornes du condensateur
en respectant les conventions indiquées sur le schéma.

d. Entre les instants de dates tA et tB (voir la figure ci-dessus), le condensateur se charge-t-il
ou se décharge-t-il? Justifier la réponse.
e. À partir de la courbe traduisant uC(t), et en utilisant la relation établie à la question c),
retrouver la valeur de i à l'instant tA et le sens réel de circulation du courant entre tA et tB.
2. Étude énergétique
On souhaite étudier l'énergie totale E de l'oscillateur électrique. Cette énergie est la somme de
l'énergie électrique E1=1/2.C.uC2 emmagasinée dans le condensateur et de l'énergie magnétique
E2=1/2.L.i2 emmagasinée dans la bobine. Le logiciel utilisé peut calculer, à partir des mesures, les
valeurs de ces trois énergies et fournir les courbes donnant leur variation en fonction du temps.
a. L'origine des dates étant la même pour toutes les courbes, identifier les trois courbes
données ci-dessus en ne justifiant que l'identification de la courbe donnant les variations
de l'énergie magnétique.
b. Interpréter brièvement la décroissance de l'énergie totale de l'oscillateur électrique.
II. Modélisation
On suppose maintenant que l'oscillateur ne comporte aucune résistance. Dans ces conditions, la
tension uC aux bornes du condensateur est de la forme:
uC(t) = Um sin(ω0t + Ф)
avec
ω0 =
2π
=
1
T0
où T0 est la période propre de l'oscillateur.
1. Calculer la valeur de T0.
2. Établir les expressions:
o de l'énergie électrique en fonction de C, Um, ω 0, Ф et t;
o de l'énergie magnétique en fonction de C, Um, ω0, Ф et t.
3. Montrer que, dans ce cas, l'énergie totale de l'oscillateur est conservée.