Etablir l`expression de l`accélération subit par une particule dans le

jeudi 3 décembre 2009
Devoir 1ière I,1 b
Exercice 1 (8 points)
Etablir en détail l’expression de l’accélération pour une particule de masse m qui effectue un
mouvement circulaire uniforme.
Exercice 2 (4 + 1 + 6 = 11 points)
a. Enoncer la loi de gravitation de Newton sous sa forme vectorielle après avoir fait une
figure soignée. Expliquer toutes les grandeurs physiques qui y interviennent et donner
leur unité.
b. Donner la définition du vecteur « champ de gravitation ».
c. On veut placer un satellite sur une orbite géostationnaire autour de Jupiter
(M=1,9·1027kg; R=71 400km; T=9h51min). Etablir et calculer le rayon r et l'altitude z
de la trajectoire.
Exercice 3 (3 + 6 + 2 + 6 + 5 = 22 points)
a. Enoncer la troisième loi de Kepler ! (Texte + Formule)
b. Etablir soigneusement (figure, référentiel, repère e.c.t.) l’expression de la constante
intervenant dans la troisième loi de Kepler en fonction de K et M, à partir des forces
qui s’exercent sur un corps se trouvant en obit circulaire autour d’un astre de masse M.
c. Mars a deux petits satellites naturels. Phobos, le plus grand, a un rayon de 11.5km
pour une masse de 13,4·1015kg.
i. Calculer l'intensité du champ de gravitation à la surface de Phobos.
ii. Quelle vitesse faut-t-il donner à une balle de golf de 46g pour qu'elle gravite
autour de Phobos sur une trajectoire circulaire au ras du sol?
iii. Phobos, se trouve sur une orbite quasi circulaire de rayon r=9380km et de
période T=7h39min. Déduire la masse de la planète Mars.
Exercice 4 Vrai ou faux? Motivez vos réponses. Redressez si possible. (8 points)
a. Dans un mouvement circulaire, le vecteur accélération tangentielle
T
a
peut être dirigé
en sens inverse du mouvement.
b. Le mouvement d'un projectile se déplaçant dans un champ de pesanteur dépend de sa
masse.
c. Deux planètes ayant même champ de gravitation à leur surface ont même masse.
d. Un satellite en orbite circulaire autour de la Terre est soumis à une force constante.

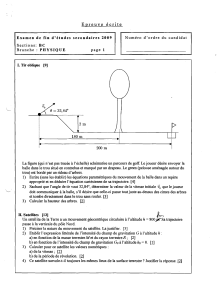
Exercice 5 (5 + 2 + 4 = 11 points)
Une source de protons émet des protons
qui sont accélérés de L1 vers L2 et
traversent le trou en L2 avec des vitesses
variables.
Toute la région à droite du diaphragme L2
baigne dans un champ B uniforme de
75mT. Entre les diaphragmes L2 et L3 il
règne en plus un champ électrique E créé
par un condensateur (dessiner en gras).
Derrière L3 on n'a plus que le champ
magnétique.
a) Expliquer pourquoi la présence simultanée de E et de B permet aux protons qui ont une
certaine vitesse de passer en ligne droite de L2 vers L3. Déterminer les caractéristiques des
vecteurs
E
et
B
.
b) La vitesse des protons qui passent en ligne droite vaut 5,15·105m/s.
i. Calculer l'intensité du champ E dans le condensateur se trouvant dans la région
entre L2 et L3.
ii. Etablir et calculer la distance d entre le trou L3 et le point d'impact sur l'écran.
Relevé des principales constantes physiques
Charge élémentaire
e
1,60210-19
C
Masse au repos de l'électron
me
9,109410-31
5,485810-4
0,5110
kg
u
MeV/c2
Masse au repos du proton
mp
1,672610-27
1,0073
938,27
kg
u
MeV/c2
Masse au repos du neutron
mn
1,674910-27
1,0087
939,57
kg
u
MeV/c2
Masse au repos d'une particule 
m
6,644710-27
4,0015
3727,4
kg
u
MeV/c2
Grandeurs liées à la Terre et au Soleil
(elles peuvent dépendre du lieu ou du temps)
Valeur utilisée sauf
indication contraire
Accélération de la pesanteur à la surface terrestre
g
9,81
m s-2
Rayon moyen de la Terre
R
6370
km
Jour sidéral
T
86164
s
Masse de la Terre
MT
5,981024
kg
Masse du Soleil
MS
1,991030
kg
1 angström = 1
o
A
= 10-10 m
1 électronvolt = 1 eV = 1,60210-19 J
1 unité de masse atomique = 1 u = 1,660510-27 kg = 931,49 MeV/c2