Table des matières automatique

K. Zampieri – Mauris Cornelis Escher 1
Maurits Cornelis Escher
1
Sommaire
1) En bref ............................................................................................................................................. 1
2) Biographie ....................................................................................................................................... 1
3) Arts et Culture ................................................................................................................................. 2
4) Références et liens externes ........................................................................................................... 3
1) En bref
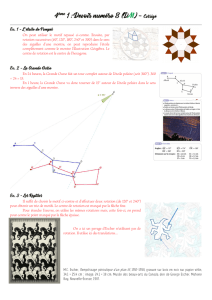
Maurits Cornelis Escher était connu pour ses gravures sur bois, lithographies
et mezzotintos, qui représentent des constructions impossibles, l'exploration
de l'infini, et des combinaisons de motifs qui se transforment graduellement en
des formes totalement différentes.
Son œuvre expérimente diverses méthodes de pavage en
2 ou 3 dimensions ou représente des espaces paradoxaux
qui défient nos modes habituels de représentation.
L'œuvre de Maurits Cornelis Escher a séduit de nombreux mathématiciens
auxquels il se défendait d'appartenir. Il aimait à dire à ses admirateurs :
« Tout cela n'est rien comparé à ce que je vois dans ma tête ! »
2) Biographie
M.C. Escher est né à Leeuwarden (Pays-Bas) en 1898, cadet de l'ingénieur hydraulique G. A.
Escher. En 1903, la famille déménagea à Arnhem. En 1919, Escher intégra l'École d'architecture
et des arts décoratifs de Haarlem ; il étudia brièvement l'architecture, mais se dirigea vers les arts
décoratifs, étudiant sous la direction de Samuel Jesserun de Mesquita.
Il voyagea régulièrement en Italie et c'est là qu'il rencontra la femme qu'il épousera en 1924, Jetta
Umiker. Le jeune couple s'installa à Rome, y resta jusqu'en 1935 et lorsque le climat politique
sous Mussolini devient insoutenable, ils déménagèrent en Suisse.
Escher, très épris des paysages italiens qui étaient sa source d'inspiration, n'était pas heureux en
Suisse et déménagea donc en 1937 à Uccle, une des grandes communes de la Région de
Bruxelles-Capitale en Belgique. La Seconde Guerre mondiale le força à déménager en janvier
1941, à Baarn aux Pays-Bas, où il vécut jusqu'en 1970. Enfin Escher intégra la maison de retraite
pour artistes de Rosa-Spier à Laren en 1970, une maison où il put avoir un atelier pour lui, et y
mourut le 27 mars 1972.
1
Artiste néerlandais (17 juin 1898 - 27 mars 1972)
Titre
Note de bas
de page
Recopie de la mise en forme des
caractères du Style Titre1
Table des matières automatique
Guillemets

K. Zampieri – Mauris Cornelis Escher 2
3) Arts et Culture
scher, lors d'un voyage à Grenade en Espagne, est séduit
par les mosaïques Maure du palais de l'Alhambra. Il est
fasciné par ces dessins qui répètent des formes géomé-
triques des plus complexes, tant en étant des plus attrayants à l'oeil.
S'inspirant de ces mosaïques arabes, il décide de représenter des
êtres vivants dans ses gravures (contrairement aux peintures et des-
sins arabes où il est interdit de représenter les êtres vivants). La
plupart de ses dessins et gravures présentent cette idée de patrons qui s'imbriquent l'un dans
l'autre.
ans ses écrits, Escher indique qu'il recherche une façon de représenter sur papier le
concept qu'en dehors d'un univers il pourrait y avoir le néant tout autant que l'infini,
concept qu'il a eu de la difficulté à représenter pendant longtemps. En 1954, il ren-
contre le mathématicien canadien Donald Coxeter (1907-) à qui il expose son problème. Donald
Coxeter lui présente alors le cadre mathématique qui allait lui permettre de répondre à ses at-
tentes : la géométrie hyperbolique, le même concept utilisé par Einstein dans le développement
de sa théorie de la relativité générale. Grâce à cet outil mathématique, Escher réalise alors ses
gravures les plus fascinantes.
a géométrie hyper-
bolique a été in-
ventée vers 1820.
Ce fut le grand mathémati-
cien Henri Poincarré qui
en a donné une représenta-
tion visuelle. Elle corres-
pondait parfaitement à ce
que Escher cherchait, soit
représenter un univers à
l'intérieur d'un cercle, dans
lequel la périphérie repré-
senterait l'horizon et l'exté-
rieur, le néant. Il réussit ce
tour de force en dessinant
des objets qui changent de
volume au fur et à mesure
que ces objets s'approchent
de la périphérie. Ils rapetis-
sent de plus en plus au fur
et à mesure qu'ils s'appro-
chent de cet horizon vir-
tuel, donc de l'infini. La
grande difficulté pour
Escher était de déterminer
la position des points de
symétrie. En d'autres mots,
il fallait que ces objets
maintiennent leur cohé-
rence et leur forme même
s'ils rapetissaient.
E
D
L
Lettrine

K. Zampieri – Mauris Cornelis Escher 3
e grand intérêt d'Escher à l'égard des mathématiques et de la géométrie hyperbolique, de
la géométrie non-euclidienne, et autres, est évident dans toutes ses Œuvres. On retrouve
dans ses gravures, dessins, esquisses des formes paradoxales, des mosaïques, des mouve-
ments perpétuels, des représentations impossibles, des polyèdres dans lesquels les repères natu-
rels des formes et la logique de l'espace sont totalement redéfinies relativement aux formes et à
l'espace naturelles.
Tripoutre, objet improbable
Principe de la supercherie
4) Références et liens externes
http://mcescher.frloup.com/ (extrait - (fr) Le Monde étrange de M.C. Escher)
http://www.mcescher.com/ (en) (Site officiel de M.C. Escher)
http://people.via.ecp.fr/~jm/musee/escher.html (fr) (Musée de M.C. Escher)
http://les-mangeurs-dimages.blogspot.com/2007/03/escher-et-lescalier-de-penrose.html (fr)
(deux vidéos sur une analyse de la lithographie Ascending et descending)
L
Tableau 2×2
Hyperliens actifs
Pied de page : Prénom Nom ; Sujet – A
Droite : numéro de page
Impératifs : Les images sont à placer dans les
paragraphes correspondants ; Habillage au choix.
Coupure des mots activée.