chap5-lois_de_newton_exos_2s

2S Cours Physique
Chap5 : Les 3 LOIS de NEWTON et le mouvement d’un solide : EXERCICES
Dans ce chapitre, vous devez utiliser la méthode de résolution d’un exercice p7 et donc faire des projections. Vous n’avez pas le
droit d’utiliser la méthode du « triangle qui se referme » du chapitre précédent !
Ex1 : ressort de moi, esprit maléfique !
Un solide S de poids P = 10,0 N est posé sur une table inclinée d'un angle
= 30° avec l'horizontale. Le contact entre le solide et le table est supposé
sans frottements. Le solide est maintenu en équilibre sur la table grâce à un
ressort dont l'axe est parallèle à la table et de raideur k = 200 N/m.
1) Déterminer la valeur de la réaction de la table sur le solide S. Vous
donnerez 2 chiffres significatifs.
2) Calculer l'allongement du ressort. Vous donnerez 2 chiffres
significatifs.
Ex2 : valise Taylor ?
Un voyageur tire une valise de masse m = 8,50 kg sur un sol horizontal, à l'aide d'une corde.
La direction de la corde fait un angle = 30,0° avec l'horizontale. La valise glisse en ligne droite et sa vitesse est constante.
La tension de la corde a pour valeur T = 60,0 N. On prendra g = 9,80 N/kg
1) Trouver l’intensité de toutes les forces. Vous donnerez 3 chiffres significatifs.
2) Représenter ces forces à l’échelle 1cm représente 20 N.
Ex3 : un traîneau…stalgique !
Le traîneau du Père Noël de masse M = 120 kg, tiré par ses rennes, glisse à vitesse constante, sur un sol horizontal. Les rennes
exercent une force de 400 N sur la corde qui fait un angle = 30° avec l’horizontale. On donne g = 10 N/kg.
1) Il y a-t-il des frottements entre le sol et le traîneau ?
2) Représenter précisément l’action du sol sur le traîneau notée
R
, par une
construction graphique (échelle 1 cm représente 400 N).
3) Déterminer l’intensité R de l’action du sol sur le traîneau, ainsi que
l’angle que fait cette force avec la verticale.
Ex4 : un exercice coton …pour une tige !
Une tige OB (Stange) de masse m = 5,0 kg et de longueur l = 1,0 m est retenue en B par un fil dont
la tension vaut : T = 20 N.
A l’équilibre, le fil est perpendiculaire à la tige OB.
On donne AB = 1,0 m et g = 10 N/kg.
1) Faire un bilan des forces extérieures appliquées à la tige.
2) Ecrire la condition d’équilibre.
3) Représenter précisément l’action du mur en O sur la tige, notée
O
R
, par une construction
graphique.
Echelle 1 cm représente 10 N.
4) Déterminer l’intensité RO de l’action du mur en O sur la tige, ainsi que l’angle que fait cette
force avec la tige, en projetant la condition d’équilibre sur les axes du repère dessiné.
Ex5 : ah…scenseur !
Une cabine d'ascenseur de masse M = 300 kg transporte une charge de masse m = 200 kg. Le câble exerce
sur la cabine une tension T d'intensité 5900 N. Immobile au départ, la cabine monte. On prendra g = 9,80
N/kg.
1) Calculer l’accélération de la cabine. On donnera 3 chiffres significatifs.
2) Quelle est la nature du mouvement de la cabine ?
3) Au bout de combien de temps la vitesse de la cabine sera de 20,0 km/h. On donnera 3 chiffres
significatifs.
4) Le câble casse. Calculer la nouvelle accélération de la cabine. On donnera 2 chiffres significatifs.
5) Au bout de combien de temps la vitesse de la cabine sera de 20,0 km/h ?
O
x
y
fil
tige
B
A
mur

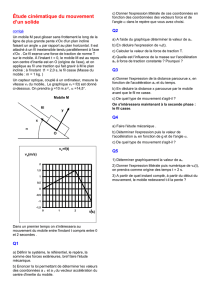
Ex6 : prendre la tangente
L’expression « prendre la tangente » signifie partir, se sauver,
s’esquiver…Mais d’où vient-elle ? L’étude d’un mobile sur une table à
coussin d’air peut en donner une idée.
Le mobile est accroché à un fil inextensible dont l’autre extrémité est liée à un
point fixe O. Le mobile est lancé à t0 avec une certaine vitesse v0.
A un moment donné, le fil casse.
On étudie le mouvement de son centre d’inertie C dans le référentiel terrestre.
L’enregistrement de droite est à l’échelle réelle. La durée entre deux positions
consécutives est de = 28 ms.
1) Quelle est la nature du mouvement ? (2 phases)
2) A quel instant le fil casse ? Quelle direction prend le mobile au moment de la rupture du fil ?
3) Phase 1 : avant la rupture du fil.
a) Le principe d’inertie est-il respecté ? Vérifiez votre réponse par un bilan des forces effectué sur un schéma clair.
b) Calculer les valeurs des vitesses instantanées v1 et v3 en m/s.
c) Ecrire la 2ème loi de Newton pour le mobile (PFD).
d) En projetant le PFD sur un axe pratique, trouver la valeur de l’accélération du mobile sachant que sa masse est
m = 600 g et que la valeur de la tension du fil est T = 0,096 N.
4) Phase 2 : après la rupture du fil.
Le principe d’inertie est-il respecté ? Vérifiez votre réponse par un bilan des forces effectué sur un schéma clair.
Ex7 : was für ein Lüge ?
Une luge de masse m = 8,0 kg est lâchée sans vitesse initiale en haut d'une piste enneigée faisant un angle de = 12° avec
l'horizontale. On prend g = 9,8 N/kg et on néglige tous les frottements dans un premier temps.
1. Faire le bilan des forces agissant sur la luge.
2. Caractériser le mouvement du centre d’inertie de la luge.
3. Calculer la valeur de la réaction de la piste.
4. Calculer la valeur de l’accélération du centre d’inertie de la luge.
5. En supposant cette accélération constante, calculer la durée mise par la luge pour
atteindre la vitesse de 50 km/h.
6. Même question si la luge est lancée en haut de la piste avec la vitesse v0 = 20 km/h.
7. En réalité, la luge frotte sur la neige. Initialement immobile, elle met 12,4 s pour
atteindre la vitesse de 50 km/h. Calculer la valeur de l’accélération du centre
d’inertie de la luge.
8. En déduire la valeur supposée constante de la force de frottement notée f de la
neige sur la luge.
Ex8 : plan incliné
Sur un aérobanc, incliné d'un angle  par rapport à l'horizontale, un mobile à
coussin d’air de masse M est entraîné dans un mouvement ascendant par un
contrepoids de masse m. Le mobile et le contrepoids sont reliés par un fil
inextensible de masse négligeable qui passe dans la gorge d'une poulie de
masse négligeable. La poulie ne fait que transmettre la tension du fil.
Un dispositif informatique permet de calculer les vitesses instantanées du centre
d’inertie du mobile.
On donne : M = 50,4 g ; m = 20,0 g ; g = 9,81 m/s²; = 12°.
1) A partir du graphe v = f(t) déterminer la nature du mouvement du mobile, la
vitesse à la date t = 0 et son accélération.
2) Etude du contrepoids :
- Représenter sur un schéma les forces extérieures appliquées au contrepoids.
- Exprimer la valeur de la tension du fil T en fonction de m, g et de
l'accélération ac du contrepoids.
3) Etude du mobile :
- Représenter sur un schéma les forces extérieures appliquées au mobile. La tension du fil sera notée T1.
- Exprimer la valeur de la tension du fil T1 en fonction de M, g, et de l'accélération a du mobile.
4) Synthèse : on peut montrer que les tensions T et T1 sont égales, dans la mesure où le fil inextensible et la poulie ont des masses
négligeables devant m et M.
- Etablir l'expression littérale de l'accélération a du mobile en fonction de m, g, M et .
- Calculer cette accélération en donnant 3 chiffres significatifs.
5) Equilibre : calculer la valeur de l’angle pour que le mobile et le contrepoids restent en équilibre.

2S Cours Physique
Chap5 : Les 3 LOIS de NEWTON et le mouvement d’un solide : EXERCICES
Dans ce chapitre, vous devez utiliser la méthode de résolution d’un exercice p7 et donc faire des projections. Vous n’avez pas le
droit d’utiliser la méthode du « triangle qui se referme » du chapitre précédent !
Ex9 : application du PFD
Cet exercice étudie un modèle très simplifié du mouvement du centre d'inertie G d'un skieur.
L'ensemble des forces de frottement du sol est assimilé à une force unique, de sens opposé au vecteur vitesse, de norme constante
RT = f = 50 N. On négligera les frottements de l’air.
Données : masse du skieur m = 80 kg, g = 9,8 m/s2
Démarrage horizontal : initialement immobile (v0 = 0,0), le skieur s'accroche à une perche
faisant un angle = 40° avec l'horizontale. La perche exerce une force de traction supposée
constante T = 91 N. Après un parcours rectiligne et horizontal de durée 8,0 s, la vitesse se
stabilise à la valeur v1.
a. Calculer l'accélération ax supposée constante du skieur durant la phase de démarrage
en donnant 2 chiffres significatifs. Prendre ax = 0,30 m/s2 pour la suite si vous n’avez pas
trouvé.
b. En déduire la valeur de la vitesse v1 atteinte au bout de 8,0 s. Donner 2 chiffres
significatifs.
c. Quelle serait la valeur de la vitesse v1 atteinte au bout de 8,0 s en l’absence de tout
frottement ? Donner 2 chiffres significatifs.
x