Etape 6. Décomposer, lire et écrire des grands nombres Objectifs

Etape 6. Décomposer, lire et écrire des
grands nombres
Objectifs
Savoir-faire : Lire et écrire des grands nombres (au-delà du million).
Savoirs : Les « classes » (unités, mille, millions). Relations entre rangs et classes.
Description : Pour amener les élèves à comprendre le fonctionnement de la numération
parlée des grands nombres (par classes), il est proposé un premier jeu de commandes en
unités, milliers et millions. La deuxième activité introduit la lecture des grands nombres dans
le sens le plus aisé (écriture en chiffres → oral) ce qui permet de montrer le lien avec les
décompositions précédentes. La troisième activité (écriture en chiffres → oral) permet de
travailler les principales difficultés des élèves : les 0 qui ne s’entendent pas.
Matériel :
Affiche avec des cubes : unité, millier, million.
Une ardoise pour chaque élève.
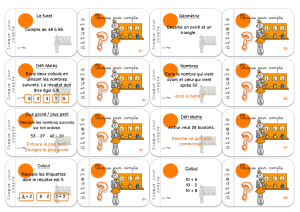
Première étape : jeu de commandes (décomposer un grand nombre)
Présentation. L’enseignant rappelle le principe du jeu de commande : le « marchand »
possède des cubes, des milliers de cubes et des millions de cubes. Il faut passer une
commande pour obtenir le nombre demandé.
Affiche présentée aux élèves (voir dernière page) :
1 unité
1 millier
1 million
http://blog.nathanielraley.com/2014/06/base-ten-blocks-to-billion.html
Le problème. L’enseignant écrit un nombre au tableau sans trop marquer les espaces entre
les classes (par exemple 2 105 086, 35 002 712, …) et demande aux élèves d’écrire sur leur
ardoise (ou cahier) le nombre de cubes à l’unité, le nombre de cubes par milliers et le
nombre de cubes par millions pour obtenir le nombre indiqué. Le nombre n’est pas lu (le
travail sur la façon de lire le nombre est l’objet de la partie suivante).
Mise en commun et vérification. Lors de la mise en commun l’enseignant recueille les
différentes réponses proposées par les élèves et les amène à échanger sur leur validité.
La vérification revient au travail fait dans la situation précédente (dénombrement de
grandes collections). Elle peut se faire en repassant d’une écriture en classes à une écriture
en unités. Par exemple la réponse 2 millions 105 milliers 86 unités peut être écrite ainsi :
2MM 1CM 5M 8D 6U, ce qui permet de retrouver l’écriture en chiffres 2 105 086.
Le tableau de numération permet de rappeler la position des différentes unités dans
l’écriture en chiffres.
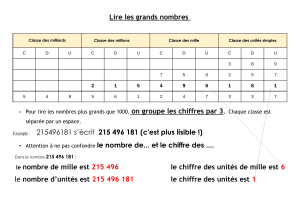
Deuxième étape : lire des grands nombres.

L’enseignant écrit un nombre en chiffres (par exemple 3 045 807, 18 006 030, …) au tableau.
Les élèves doivent le lire « dans leur tête » et il interroge un élève qui dit ce qu’il a trouvé.
Les autres disent s’ils ont le même nombre ou pas.
Discussion et synthèse : l’enseignant fera le lien entre la décomposition en millions, milliers
et unités (cf. première étape) et la lecture du nombre.
Remarque : cette étape est courte (trois ou quatre nombres proposés), le but étant de
confronter rapidement les élèves à l’étape suivante.
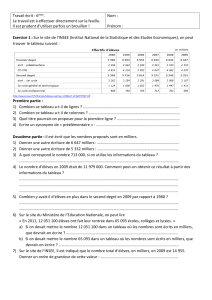
Troisième étape : Ecrire des grands nombres en chiffres
Le problème. L’enseignant écrit un nombre en chiffres (par exemple 1 002 054) au dos du
tableau (ou sur une ardoise).
Un élève vient lire ce nombre sans le montrer aux autres, mais pour que les autres puissent
le retrouver.
Les autres élèves doivent alors écrire sur leur ardoise le nombre cherché.
Choix des nombres. Les nombres sont choisis avec des zéros à certains rangs (par exemple
1 002 054, 47 080 309, 651 000 004, …) pour travailler sur la principale difficulté : les zéros
que l’on n’entend pas à l’oral.
Discussion collective. L’enseignant recueille les différentes réponses au tableau (de façon à
ce que quand on ouvrira la partie cachée les deux parties soient côte à côte). Les élèves
doivent se mettre d’accord sur une seule réponse. Les discussions doivent amener à lire des
nombres pour les invalider ou faire référence au rang des milliers, des millions, … Le tableau
de numération peut aider.
Une fois tout le monde d’accord, l’élève au tableau montre le nombre de départ et on
compare les deux écritures. L’élève qui a lu le nombre a pu aussi faire une erreur …
Un autre élève prend sa place et l’activité se poursuit avec un autre nombre.
Autre dispositif possible : avec un logiciel de dictée vocale sur ordinateur ou téléphone
portable de l’enseignant (possible avec Google Translate® qui est gratuit : on écrit en chiffres
dans le mode « anglais » mais sans espace ni point ni virgule, et on demande la traduction en
français avec dictée vocale). Du coup on fait discuter les élèves et après on fait lire par le
logiciel les différentes propositions pour vérification.
Eléments de synthèse : pour lire/écrire un grand nombre
La lecture des grands nombres s’appuie sur une décomposition en « classes » : millions,
milliers et unités. Pour les milliers on dit « mille » et pour les unités on ne dit rien.
Par exemple : 403 012 068 peut se décomposer en 403 millions 12 milliers 68 unités. Ce
nombre se lit « quatre-cent-trois-millions-douze-mille-soixante-huit ».
Classe des millions
Classe des milliers
Classe des unités simples
CM
DM
M
CM
DM
M
C
D
U
4
0
3
0
1
2
0
6
8
Quatre-cent-trois millions douze mille soixante-huit
Quand on écrit en chiffres, on écrit un espace entre les classes pour faciliter la lecture :
403 012 768.

Exercices d’entraînement
On trouve ce genre d’exercices facilement dans les manuels ou sites internet.
Exemple :
1. Ecris ces nombres en lettres
30 256 : ………………………………………………………………………………………………………………………………
78 054 : …………………………………………………………………………………………..…………………………………
321 006 : …………………………………………………………………………………………..………………………………
820 000 : …………………………………………………………………………………………..………………………………
1 005 251 : …………………………………………………………………………………………………………………………
765 203 015 : ……………………………………………………………………………………………………………………
820 002 900 : …………………………………………………………………………………………..…………………………
2 : Ecris ces nombres en chiffres :
Cinq-cent-quatre-vingt-mille-cinq : …………………………………
Huit-cent-trente-deux-mille-neuf-cent-cinq : …………………………………
Trois-millions-quatre-cent-cinquante : …………………………………
Quatre-vingt-dix-huit-millions-quatre-cent-mille : …………………………………
Neuf-cent-soixante-seize-millions-huit-cent-mille-trois : …………………………………
Trois-cent-quarante-et-un-millions-deux-cent-trois : …………………………………

1 unité
1 millier
1 million

http://numerationdecimale.free.fr