III. « Catch and shoot » et « buzzer beater »

17/04/2017 769804487 1/4
TS
Dérivées et primitives – Application au mouvement parabolique
AP
I. Détermination d’une dérivée
 Déterminons par exemple une vitesse à partir …
1. D’un vecteur position
 On utilise la relation
Error!
=
Error!
 Si
Error!
Error!
alors
Error!
Error!
 Et la vitesse, à la date t = 2,0 s, vaut alors :
║
Error!
║ =
Error!
= ……………………………………
2. D’un relevé de positions On utilise la relation
Error!
=
Error!
Ainsi, la vitesse au point M3 est : ║
Error!
║ = v3
Error!
3. D’un graphe
3.1. On détermine la pente de la tangente à la date
désirée. Ainsi, la vitesse du mobile selon l’axe
(Ox) à la date
t = 12,0 s est :
pente =
Error!
=
Error!
= .........................
 La pente de la tangente au point d’abscisse t d’une courbe donne la valeur du nombre dérivé à cette date.
 Questions
3.2. Quelle est la grandeur que l’on calcule en
déterminant la pente de la tangente à la courbe
v = f(t) ? ................................................
3.3. Déterminer graphiquement la valeur de cette
grandeur dans les unités S.I. à la date t = 0 s.
3.4. D’après le graphe que devient cette grandeur
pour un temps  20 min ? Justifier.
...............................................................................................................................................................
...............................................................................................................................................................
Position x Vitesse v Accélération a
Dérivation
Dérivation
Intégration
Intégration
t (s)
x (cm)
0 2 4 6 8 10
1
2
Soit f(x) : f = 3 x
La dérivée de f(x) s’écrit f ’(x) ou
dxxfd )(
Soit x(t) : x = 3 t
La dérivée de x(t) s’écrit
dttxd )(
Question : si  = 40 ms, que vaut v3 d’après le relevé de positions ci-contre
1
2
t (min)
v (m/s)
0 2 4 6 8 10

17/04/2017 769804487 2/4
II. Détermination d’une primitive
1. Questions
1.1. Quelle est la dérivée par rapport au temps t de 3t + 2 ? ................................................
1.2. Même question pour 3t – 5 ? ................................................
1.3. Conclure.
...............................................................................................................................................................
2. Exercice
2.1. Parmi les fonctions suivantes encercler celles qui, lorsqu’on les dérive,
donnent (t). :
3,0 t + 2,0
t + 2,0
2,0 t - 5,0
2,0 t 2 - 5,0
t 2
t 2 + 2,0 t + 1,0
2,0 t + 1,0
2.2. Donner une formule générale des fonctions qui, lorsqu’on les dérive, donnent (t).
...............................................................................................................................................................
2.3. Parmi les fonctions encerclées en existe-t-il une qui peut être égale à (t) ? Si oui laquelle ? Si non
pourquoi ?
...............................................................................................................................................................
...............................................................................................................................................................
2.4. Donner l’expression correcte de la fonction (t) telle qu’attendue par l’énoncé.
...............................................................................................................................................................
...............................................................................................................................................................
2.5. Donner une formule générale de la fonction v(t) : ................................................
2.6. D’après cette expression, que vaut v à l’origine du temps ? ................................................
2.7. Si l’on sait qu’à l’origine du temps la valeur de v est égale à 3,0 m.s-1, donner alors l’expression générale de
la fonction v(t) : ...............................................................................................
2.8. Que vaut v à la date t = 12 s ?
...............................................................................................................................................................
2.9. Sachant que la fonction z(t) est telle que si on la dérive on obtient -9,8 t + 3,0, que faut-il faire pour trouver
l’expression de z(t) ? ................................................
2.10. Parmi les expressions suivantes, encercler celle ou celles qui peuvent exprimer z(t) :
-9,8t² + 3,0t – 1,0
-9,8t² + 3,0
-4,9t² + 3,0t
-4,9t² + 3,0
-4,9t² + 3,0t – 7,0
-9,8t² + 3,0t – 7,0
-4,9t² + 9,8
-9,8t² + 3,0t
-4,9t² + 3,0t + 4,5
-9,8
2.11. Que faut-il alors connaître pour pouvoir choisir la bonne expression de z(t) ?
...............................................................................................................................................................
2.12. On sait qu’à l’origine du temps le mobile est à l’origine du repère. Déterminer l’expression correcte de z(t).
...............................................................................................................................................................
Alpha (t) Beta (t)
Dérivation
Intégration
Formule générale pour la dérivée :
n
t
1
n tn
Formule générale pour la primitive :
n
t
 ………………..
 Soit une fonction (t) telle que si on la dérive on obtient la fonction (t).
 On sait qu’à l’origine du temps (t = 0) la valeur de  est égale à 3,0.
 On sait aussi que la fonction (t) s’écrit : (t) = 2,0.
 Soit une fonction v(t) telle que si on la dérive on obtient la fonction a(t).
 On sait que la fonction a(t) s’écrit a(t) = -9,8 dans les unités S.I.

17/04/2017 769804487 3/4
III. « Catch and shoot » et « buzzer beater »
 Pour vous aider si besoin, voir ce buzzer beater rennais (30/01/16) :
https://www.youtube.com/watch?v=ejaG0IHsIRU
« Les personnages et les situations de ce récit étant purement fictifs, toute ressemblance avec des personnes ou des
situations existantes ou ayant existé ne saurait être que fortuite. »
 Aux Etats-Unis en 2015, lors d’un match de basket entre l’équipe des éperons et celle des jazzmen, le score est de
98 à 100 pour les jazzmen. Il reste 1,30 s avant la fin du match.
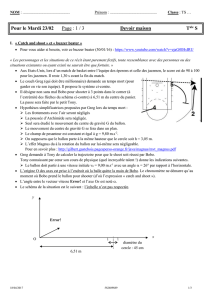
 Le coach Greg (qui doit être millionnaire) demande un temps mort (pour
garder en vie son équipe). Il propose le système ci-contre.
 Il désigne non sans mal Bobo pour shooter à 3 points dans le corner (à
l’extrémité des flèches du schéma ci-contre) à 6,51 m du centre du panier.
La passe sera faite par le petit Tony (1,88 m quand même).
 Hypothèses simplificatrices proposées par Greg lors du temps mort :
 Les frottements avec l’air seront négligés
 La poussée d’Archimède sera négligée.
 Seul sera étudié le mouvement du centre de gravité G du ballon.
 Le mouvement du centre de gravité G se fera dans un plan.
 Le champ de pesanteur est constant et égal à g = 9,80 m.s-2.
 On supposera que le ballon parte à la même hauteur que le cercle soit h = 3,05 m.
 L’effet Magnus du à la rotation du ballon sur lui-même sera négligeable.
 Greg demande à Tony de calculer la trajectoire pour que le shoot soit réussi par Bobo.
Tony connaissant par cœur son cours de physique (quel incroyable talent !) donne les indications suivantes.
 Le ballon doit partir à une vitesse initiale v0 = 9,00 m.s-1 avec un angle  = 26° par rapport à l’horizontale.
 L’origine O des axes est prise à l’endroit où la balle quitte la main de Bobo. Le chronomètre ne démarre qu’au
moment où Bobo prend le ballon pour shooter d’où l’expression « catch and shoot ».
 L’angle entre le vecteur vitesse
Error!
et l’axe Ox est noté .
 Le schéma de la situation est le suivant : l’échelle n’est pas respectée.
O
y
x
6,51 m
Error!
diamètre du
cercle : 45 cm

17/04/2017 769804487 4/4
Source de la photo : A. B.
Vérification des calculs de Tony
1. Force(s) exercées sur le ballon
1.1. Préciser le référentiel à utiliser ainsi que le système.
1.2. En utilisant les hypothèses simplificatrices, quelle(s) est (sont) le(s) force(s) qui s’applique(nt) sur le ballon ?
2. Equation de la trajectoire
 Les conditions initiales du mouvement sont à t = 0 ;
Error!
(t = 0) =
Error!
et pour x(t = 0) = 0, y(t = 0) = 0
2.1. Rappeler à Tony l’énoncé de la deuxième loi de Newton.
2.2. En appliquant la deuxième loi de Newton, démontrer que les équations horaires du mouvement de G
s’écrivent : le détail du raisonnement est indispensable.
Error!
Error!
2.3. Montrer que l’équation de la trajectoire peut se mettre sous la forme y(x) = -
Error!
Error!
 x² + tan()  x.
2.4. En utilisant les données, trouver une expression numérique de la trajectoire y(x).
2.5. Tracer, à l’aide de la calculatrice, la représentation graphique de la trajectoire y(x).
3. Buzzer beater ?
3.1. D’après le graphique précédent, le panier est-il marqué ? Justifier.
3.2. A partir de l’expression générale de y(x), démontrer que la portée du ballon, définie par l’abscisse xP tel que
y(xP) = 0, peut se mettre sous la forme xP =
Error!
. Donnée : 2 sin()  cos() = sin(2).
3.3. Quelle est la durée t du shoot ? Le chronomètre affichera-t-il 0,00 s quand le ballon rentre dans le panier.
On supposera que Bobo met 0,50 s entre la réception du ballon et le départ du ballon.
4. Ce que n’avait pas prévu Tony … et Greg
 Un grand joueur des jazzmen, R.G., se détend pour atteindre une hauteur H = 3,75 m (du bout des doigts) par
rapport au sol. R.G.est situé à 2,0 m de Bobo au moment du départ de la balle.
4.1. Identifier R.G.
4.2. Discuter sur l’éventualité du contre.
4.3. Bobo, voyant arriver R.G., décide de changer un paramètre de son shoot pour éviter le contre.
Quel paramètre du shoot peut-il « facilement » changer ? Quelle sera la nouvelle valeur de ce paramètre ?
4.4. Quelle est la durée t’ du shoot ? L’arbitre Jacques va-t-il accorder le panier ? On suppose toujours que
Bobo met 0,50 s entre la réception du ballon et le départ du ballon.
5. Retrouvailles (Question bonus)
 Les trois joueurs se sont retrouvés ensemble en 2015 lors de
quelques matchs.
Préciser les noms des 5 joueurs de la photo ci-contre.
Donner le lieu et la date de ce match
Indice : la photo a été prise un samedi.