Leçon 33

Leçon 33
Exemples de couplage électromécanique : haut-parleur électrodynamique,
moteurs... Bilans énergétiques (PC, PSI)
--------------------
Bibliographie : fait un peu double emploi avec la leçon 19. Donc la bibliographie est la même. En règle
générale, rechercher les chapitres « Applications de l’induction ». Attention aux problèmes de signe
dans toutes les collections (sauf Hachette Electronique pour le moteur) ! ! D’après le programme, il faut
montrer que la somme de la puissance électrique induite & de la puissance mécanique des forces de
Laplace est nulle dans le cas d’un couplage électromécanique (pour illustrer la convention générateur
& tous les problèmes de signe qu’elle induit, voir toutes les collections !).
 Ellipses Elec 2 : chapitre 6 (bien, mais un peu sec).
 Hachette Elec 2 : chapitre 5 (pour le HP).
 Hachette Electronique II PSI (pour le moteur). Bien.
 Tec & Doc Ondes : chapitre 8. Léger !
 Dunod : Electromagnétisme II : chapitres 17. Signes un peu plus clairs. Bien.
I. HAUT - PARLEUR : attention ! Hachette part d’un résultat d’acoustique, pas vraiment électroméca-
nique.
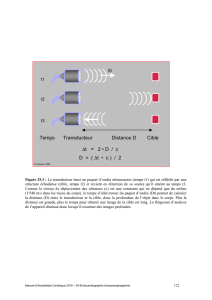
1. Le transducteur : on appelle transducteur un système qui réalise une conversion de forme
d’énergie. En toute rigueur, le haut - parleur est un double transducteur (conversion électrique - méca-
nique, puis mécanique - acoustique). La conversion d’énergie sur le transducteur sera supposée intégrale.
C’est un moteur. Du point de vue électrique, il a une résistance R, une inductance L, une fem algébrique
e, & est alimenté en énergie électrique par le générateur (E, r). Du point de vue mécanique, il est ramené
à sa position d’équilibre par un ressort de raideur k & freiné par une force visqueuse de coefficient f.
2. Equations de couplage du haut - parleur : si l est la longueur du bobinage plongée dans le
champ magnétique, la fem induite (cas de Lorentz) est donnée par
Blve 
, orientation positive selon le
courant extérieur. Alors l’équation électrique (E), homogène à des tensions, s’écrit en traduisant la loi de
Pouillet :
(E) )( dt
dI
LIRrBlvE 
. La force de Laplace est évidemment motrice & vaut
BlIF 
,
d’où l’équation mécanique (M), homogène à des forces :
(M) BlIfvkx
dt
dv
m
.
3. Bilan de puissances : pour fabriquer des puissances, on forme les combinaisons (E).I et (M).v,
soit :
dt
dI
LIIRrBlvIEII 2 )(:(E).
&
BlIvfvkxv
dt
dv
mvv 2 :(M).
, ce qui fait apparaître
le terme commun (dit de couplage)
vIBL.
. En l’éliminant, on obtient le bilan de puissances :
 2222 2
1
2
1kxmv
dt
d
fvIRrEI
, de la forme
dt
dW
PertesFournie  PP
.
La puissance fournie vaut
EI
Fournie P
, & celle dissipée dans les pertes vaut :
22
)()( fvIRrmécaélec PertesPertesPertes  PPP
, enfin le système stocke l’énergie W définie
par :
22 2
1
2
1kxmvW
. La puissance des forces de Laplace vaut
IvBlFv .
, & correspond au terme
de couplage. Elle est positive pour un moteur (force dans le sens de la vitesse) :
vIBl
L.P
. La puis-
sance électrique liée à la fem induite vaut :
vIBleI .
, d’où
vIBl
e.P
, d’où on déduit que :
0 eL PP
.

II. MOTEUR A COURANT CONTINU : H-Prépa Electronique II.
Faut-il parler de la machine à courant continu ou des moteurs synchrone & asynchrone ? La réfé-
rence au programme PC ferait pencher pour la première solution, ce que font Faroux & Hachette, El-
lipses faisant le contraire.
A. Principe & réversibilité : citer le Hachette :
 Une machine est dite à courant continu quand les grandeurs électriques sont unidirectionnelles ;
 C’est un convertisseur électromécanique rotatif réversible (moteur ou génératrice) ;
 Le fonctionnement en moteur utilise les forces de Laplace ;
 Le fonctionnement en génératrice utilise les phénomènes d’induction (cas de Lorentz) ;
B. Description : faire un schéma de la machine, ou en présenter une.
 Le circuit magnétique : il comprend le stator en acier portant les bobinages inducteurs créant le
champ magnétique. Il y a en général p paires de pôles, séparés du rotor par un entrefer étroit pour
augmenter le champ & diminuer les pertes magnétiques. Les lignes de champ sortent d’un pôle nord,
traversent l’entrefer, le noyau de fer du rotor, à nouveau l’entrefer pour entrer dans un pôle sud & se
boucler par la carcasse du stator.
 Les deux circuits électriques : le circuit inducteur a déjà été décrit. Le circuit induit est constitué de
bobinages situés dans des encoches du rotor. Signaler que l’axe des pôles est un axe de symétrie, &
l’axe perpendiculaire , appelé ligne neutre, un axe d’antisymétrie.
 Le dispositif de commutation : le circuit induit est constitué de spires rectangulaires dont les bornes
sont reliées à des balais de graphite frottant sur les lames de cuivre du collecteur qui joue le rôle de
redresseur mécanique (pas de schéma sur le H-Prépa, voir Faroux). On obtient ainsi une fcem e(t) de
signe constant ; des câblages sophistiqués & secrets permettent de diminuer son ondulation.
Remarque : dans les machines de faible puissance, le champ magnétique est produit par un aimant per-
manent.
C. Fonctionnement :
Choisir le cas simple d’une spire unique pour en déduire les courbes B(t) & e(t). Calculer la fcem pour
montrer que
 ..ke
, où est le flux utile sous un pôle (flux magnétique à travers la surface limitant
le rotor), & k la constante de construction (sans dimension) de la machine. Par application de la réversi-
bilité (rendement unité du transducteur) on en déduit que
IkIe mécaélec ....  PP
, ex-
pression du couple moteur.
D. Pertes & rendement :
Les pertes comprennent : les pertes Joule dans les deux circuits électriques, les pertes fer (hystérésis &
courants de Foucault) dans le circuit magnétique, les pertes mécaniques (frottements) & électriques
(étincelles) sur les balais. Le rendement des machines réelles est excellent, & varie de 80 % à 95 %
E. Fonctionnement en génératrice : léger !
Le fonctionnement est réversible, & peut être utilisé pour :
 Produire une tension continue ;
 Freiner un moteur avec ou sans récupération d’énergie ;
Manip : exhiber une machine. Fonctionnement en moteur. L’idéal serait de pouvoir visualiser e(t).