1. ÉnoncÉ du sujet

MINIPROJET D’INFORMATIQUE
MISSILE POURSUIVANT SA CIBLE
Melle. QUERENET Gaëlle et M.ROURE Mathieu
Promotion 2005 ING 2 M.E.
Institut Polytechnique des Sciences Avancées

Mini projet informatique : Missile poursuivant sa cible 2/7
Document réalisé à l’IPSA par Melle. Querenet et M. Roure sous la direction de Mme. Valentin
SOMMAIRE GENERAL
1. ÉNONCÉ DU SUJET 3
1.1. Le sujet 3
1.1.1. Énoncé du sujet 3
1.1.2. Résultat à obtenir 3
1.2. Logiciel à utiliser 3
2. CALCULS PREPARATOIRES 4
2.1. Énoncé du calcul 4
2.2. Calcul à l’aide de Mathlab 4
3. PROGRAMME 5
4. RESULTAT 7

Mini projet informatique
Sujet n°5 : Missile poursuivant sa cible
3/7
Document réalisé à l’IPSA par M. Roure Mathieu sous la direction de M. Cougnon
1. ÉNONCÉ DU SUJET
1.1. LE SUJET
Après lecture des sujets notre choix c’est porté sur le sujet numéro 5, intitulé « Missile
poursuivant sa cible ».
1.1.1. ÉNONCE DU SUJET
Un ensemble de courbes intéressantes sont les trajectoires décrites par un point M,
évoluant à vitesse constante, pointant sur un point B, dont on connaît le chemin. Une telle
méthode est connu sous le nom de « poursuite du chien », tout simplement parce que la
trajectoire engendrée ressemble à celle d’un chien suivant son maître. La loi de guidage d’un
missile utilisant cette méthode est connue sous le nom de « poursuite pure » : à chaque instant,
la vitesse du missile est dirigée sur la position de la cible.
1.1.2. RESULTAT A OBTENIR
On souhaite obtenir les trajectoires du missile est de l’avion, si les conditions initiales sont :
 Á l’instant t=0, le repère est centré sur le site de lancement du missile (Xm=0,Ym=0)
 Le missile à un vecteur vitesse constant de 10 m.s-1 (Vm=10)
 Á l’instant t=0, l’avion est à 100 mètres au dessus du missile (Xa=0,Ya=100)
 L’avion vole en palier à la vitesse de 5 m.s-1 (Va=5)
1.2. LOGICIEL A UTILISER
Pour mener à bien ce mini projet informatique, nous utiliserons le logiciel « Mathlab »
développé par The MathWorks, ce mini projet viendra clôturer le cours d’initialisation à
Mathlab.

Mini projet informatique
Sujet n°5 : Missile poursuivant sa cible
4/7
Document réalisé à l’IPSA par M. Roure Mathieu sous la direction de M. Cougnon
2. CALCULS PREPARATOIRES
2.1. ÉNONCE DU CALCUL
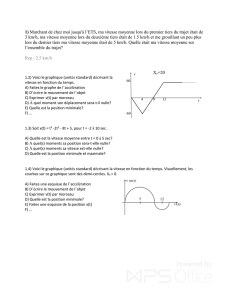
On trace pour un point quelconque du missile et de l’avion, on a le schéma suivant :
On peut appliquer le théorème de Thalès afin de déterminer la vitesse horizontale du missile :
²² dYdX
Vmissile
dX
Vx
Ce qui en sortant Vx, donne :
dX
dYdX
Vmissile
Vx  ²²
On exprime dX et dY avec les valeurs initiales :
22 YmissileYavionXmissiletVavion
XmissiletVavionVmissile
Vx
Par analogie on exprime Vy :
22 YmissileYavionXmissiletVavion
YmissileYavionVmissile
Vy
2.2. CALCUL A L’AIDE DE MATHLAB
Il suffit d’intégrer à l’aide de la fonction « ODE45 » les deux fonctions précédentes pour
obtenir une équation paramétrique de Xmissile et Ymissile ; il faut remplacer Xmissile et
Ymissile dans les équation par les fonction y(1) et y(2) qui seront calculé pas à pas par le
logiciel :
22 )2()1(
)1(
yYavionytVavion
ytVavionVmissile
Vx
22 )2()1(
)2(
yYavionytVavion
yYavionVmissile
Vy

Mini projet informatique
Sujet n°5 : Missile poursuivant sa cible
5/7
Document réalisé à l’IPSA par M. Roure Mathieu sous la direction de M. Cougnon
3. PROGRAMME
Nous avons créé le programme appelé sujet5.m, qui s’écrit de la manière suivante :
function missile
clear all;
clc;
hold off;
%Définition des constantes
%Pour l'avion
xx1=[0:1:100];
yy1=[0:1:100];
Vavion=5;
Yavion=100;
%Pour le missile
Vmissile=10;
% La trajectoire du missile
% Resolution du systeme d'equations differentielles
options = odeset('Events',@events1);
[x,y]=ode45(@eqmvt,[0:0.01:15],[0;0],options);
% La trajectoire du missile
xx1=5*x;
%Affichage
%L'avion
plot(xx1,100,'-r');
hold on;
%Le missile
plot(y(:,1),y(:,2),'X-k');
%Les axes
title 'La courbe noire représente le missile, et la rouge représente la cible'
xlabel 'Distance en mètre'
ylabel 'Altitude en mètre'
function a=eqmvt(t,y)
Vmissile=10;
Vavion=5;
Yavion=100;
%y(1)=Xmissile
%y(2)=Ymissile
a=[