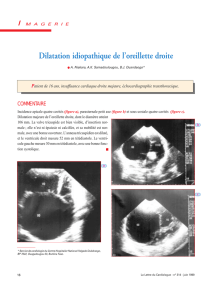
cbpt1 - Convergence

T1 Conduction,diffusion et rayonnement
I La température
1 Définition
Tout corps possède une énergie proportionnelle à une grandeur appelée Température et notée
T
2 Echelle de température
a Echelle internationale
La température peut être définie par une fonction affine ou linéaire.
La température absolue est une fonction linéaire qui ne nécessite qu’un point pour être
définie.
Par convention ce point correspond à un état très particulier de l’eau appelé « point triple de
l’eau ». En ce point on prend T=273,16 K
Son unité est le KELVIN noté K
T=0K est la température du zéro absolu. Température inatteignable mais dont sait s’approcher
très près.
b Echelles dérivées
Il existe des échelles dérivées de température qui ont été bâties sur des points fixes plus ou
moins fiables.
L’échelle Celsius est une fonction affine construite avec comme points fixes la température de
fusion de l’eau (T=0°C) et la température d’ébullition de l’eau (T=100°C)
Elle est maintenant définie en fonction de l’échelle absolue par
15,273
KC TT
L’échelle Fahrenheit est une fonction affine construite à partir de la température de l’eau salée
(0°F) et celle du corps humain (96°F).
II Transfert d’énergie
Lorsque deux corps d’énergie différente pris isolément sont mis en contact l’un de l’autre,
apparaît un transfert d’énergie du corps de plus haute énergie vers le corps de plus basse
énergie.
Ces transferts d’énergie qui cherchent à annihiler ce déséquilibre énergétique se font sous
plusieurs formes :
Travail mécanique
Travail électrique
Transfert radiatif dû aux photons et appelé rayonnement
Transfert convectif dû à un mouvement d’ensemble de la matière
Transfert diffusif dû aux mouvements d’agitation de la matière et appelé conduction

III Dilatation et thermométrie
1 Dilatation
Les corps subissant une variation de température, voient leur énergie varier.
L’énergie étant proportionnelle au volume celui varie aussi.
Dans le cas où une dimension du corps est beaucoup plus importante que les deux autres. La
variation de longueur selon cette dimension sera beaucoup plus importante et sera donc la
seule prise en compte, on parlera de dilatation linéïque :
La dilatation d’un corps est une grandeur proportionnelle à la nature du matériau (caractérisé
par une constante de dilatation) et à la variation de température.
Pour nous permettre de calculer la dilatation d’un corps on fera toujours référence à sa
longueur
0
l
à
CT  0
0
On retiendra pour la dilatation linéïque:
)( 000 TTlllT
avec λ coefficient de dilatation linéïque d’unité 1/K
et pour la dilatation volumique :
)( 000 TTlkllT
avec k coefficient de dilatation volumique d’unité 1/K et tel que :
 3k
2 Thermométrie à dilatation
La température n’est pas une grandeur directement mesurable.
On utilise la dilatation apparente d’un liquide dans son enveloppe pour connaître par
graduation de l’enveloppe la température d’un corps.
Ces thermomètres sont limités par les températures de solidification et de vaporisation des
liquides et les températures de ramollissement de l’enveloppe.
IV Chaleur
On peut quantifier l’énergie échangée lors des transferts par une grandeur appelée chaleur et
notée Q.
On remarquera que la chaleur n’est pas une grandeur intrinsèque d’un matériau mais la
mesure d’une énergie échangée.
Cette énergie échangée dépend de la masse de matériau et de la nature de celui-ci. Elle est
d’autant plus importante que la variation de température est importante.
On retiendra :
 cmQ
où Q est la chaleur d’unité le Joule J
où m est la masse de matériau d’unité le kg
et où c est la capacité calorifique massique d’unité
kgKJ

V Changements d’état
1 Définitions
2 Chaleur latente
Liquéfaction
Vaporisation
Sublimation
Solidification
Fusion
SOLIDE
LIQUIDE
GAZ
Condensation