Contraintes de dilatation.

1
Chaleur.
Chapitre 1. Température. Dilatation.
1. La température.
1.1. Grandeur thermométrique.
Pour déterminer une température, il faut utiliser un dispositif dans lequel une grandeur physique
change de valeur lorsque le dispositif se réchauffe ou se refroidit. Cette grandeur est appelée
grandeur thermométrique.
Ce peut être :
 Une longueur : pyromètre à dilatation.
 Un volume : dilatation d’un solide (anneau de S’Gravesande), dilatation d’un liquide.
 Une pression : la pression d’un gaz à volume constant.
 Une grandeur électrique : une tension, une résistance électrique…
 Une grandeur photométrique : luminance, longueurs d’onde émise.
1.2. L’échelle légale. L’échelle Celsius.
Pour définir une échelle de température, il faut établir une relation entre la grandeur
thermométrique g (longueur, pression, tension électrique…) et la température .
On choisit une fonction affine g = a. + b.
La détermination des constantes a et b nécessite deux point fixes choisis arbitrairement.
On utilise la propriété qu’ont les corps purs de changer d’état à température constante, si la
pression est maintenue constante. C’est le cas en particulier de l’eau.
Conventionnellement et de manière arbitraire.
La température de fusion de la glace sous la pression atmosphérique normale (1013
hectopascal) est choisie égale à 0°C.
La température d’ébullition de l’eau sous la pression atmosphérique normale (1013 hPa)
est choisie égale à 100°C.
On peut ainsi définir les coefficients a et b à partir des grandeurs g0 et g100. La division de
l’intervalle en 100 parties égales définit ainsi le degré Celsius. Malheureusement, à chaque
grandeur thermométrique correspond une échelle particulière. Toutes les échelles coïncident
obligatoirement à 0°C et 100°C, mais de manière plus ou moins juste pour les autres
températures.
Il a donc fallu non seulement définir les deux points fixes mais aussi la grandeur thermométrique
choisie par tous comme référence, afin de définir l’échelle légale.
C’est la variation de pression à volume constant d’un gaz dont le comportement se rapproche du
modèle théorique du gaz parfait qui fut retenue pour construire le thermomètre légal.
Le choix d’un tel gaz dépendait du domaine de températures mesuré. Le thermomètre légal
permit de déterminer un certain nombre de points fixes.
L’échelle internationale actuelle utilise maintenant 3 grandeurs thermométriques :
 de – 183°C à 630,5°C : résistance électrique d’un fil de platine
 de 630,5°C à 1063°C : force électromotrice d’un thermocouple
 au-dessus de 1063°C : la température est mesurée à partir de la lumière émise par le corps
ainsi chauffé.

2
1.3. L’échelle absolue. L’échelle Kelvin.
La pression d’un gaz parfait varie en fonction de la température exprimée en °C selon la relation
affine P = a. + b, comme il est représenté sur le graphique de la page suivante.
On peut par extrapolation définir une nouvelle échelle de température T, exprimée en kelvin K,
par une seul décalage d’origine, de façon qu’il y ait une relation de proportionnalité entre
pression et température : P = k.T.
Cette nouvelle échelle est intéressante car, contrairement à l’échelle précédente, le 0 a une
signification physique. La pression d’un gaz ne peut pas diminuer en-dessous de zéro (agitation
moléculaire nulle), il y a une limite aux basses températures. Cette limite est le zéro absolu.
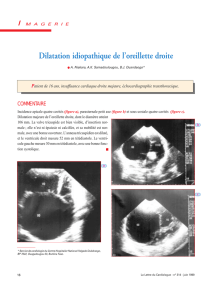
Exercice. On prend de l’eau à la température de 20°C que l’on porte à la température de 60°C.
1. Exprimer chacune de ces températures en °C.
2. Calculer la variation de température en °C () et en K (T).
 en °C, T en K, T =  + 273,15 souvent T =  + 273
T = 
Une température ne s’exprime pas par le même nombre, en °C ou en K. Par contre une
différence de température (une variation) s’exprime par le même nombre.
2. Dilatation des solides.
2.1. Données expérimentales.
On donne ici le nom de dilatation au phénomène général de variation de volume de la matière en
fonction de la température. Il peut s’agir d’une dilatation, augmentation de volume au sens
Température en °C
Température en K
0
0
100
20

3
littéraire du terme, dans le cas d’une augmentation de température ou d’une contraction,
diminution de volume, dans le cas d’une diminution de température.
Les solides se dilatent lorsqu’on les chauffe, mais se dilatent peu. Un corps creux se dilate
comme s’il était plein.
2.2. Dilatation linéaire.
Pour simplifier nous admettrons la loi de dilatation sous la forme suivante.
Au cours d’une variation de température  , la variation de longueur L est proportionnelle à la
longueur initiale L et proportionnelle à la variation de température.
L = .L.
Si la température augmente,  > 0, il vient L > 0 : la longueur augmente, il s’agit bien d’une
dilatation.
Si la température diminue,  < 0, il vient L < 0 : la longueur diminue, il s’agit en fait d’une
contraction.
Nous pouvons aussi écrire que la variation relative de longueur est proportionnelle à la variation
de température.
λ.Δθ
L
ΔL 
Le coefficient de dilatation linéaire
 L
L
1
, en K-1 (ou °C-1), est une grandeur caractéristique
du matériau.
Solide
verre de
silice
invar*
verre
Pyrex
verre
ordinaire
Pt
platinite**
Fe
Ni
Cu
Al
Zn
 (10-6 K-1)
0,6
1,2
3
8 à 9
8,7
9
11,7
12,5
16
22,4
29,7
* alliage fer-nickel caractérisé remarquable par son faible coefficient de dilatation.
** alliage fer-nickel ayant le même coefficient de dilatation que le platine et pouvant se souder
au verre, à moindre coût.
Soit L la longueur à la température , Lr celle à la température de référence r.
Nous obtenons : L-Lr=.Lr., avec  = -r d’où :
L=Lr.(1+.)
Par définition, le facteur (1   ) s’appelle binôme de dilatation linéaire.
Soit L la longueur à la température , L0 celle à la température 0°C. Il vient  = , d’où :
L = L0.(1+.)
Attention :  impérativement en °C, car il est sous-entendu  - 0.
2.3. Dilatations surfacique et volumique (cubique).
Dilatation en surface.
S = L2 = Lr2.(1 + .)2  Lr2.(1 + 2..), car . est très inférieur à 1.
Il vient donc : S = Sr.(1 + .) ou S = S0.(1 + .), avec  = 2.
, coefficient de dilatation surfacique
soit encore
θσ.
S
ΔS Δ

4
Dilatation en volume.
V = L3 = Lr3.(1 + .)3  Lr3.(1 + 3..), d’où :
V = Vr.(1 + k.) ou V = V0.(1 + k.), avec k = 3.
k, coefficient de dilatation cubique
soit encore
θk.
V
ΔV Δ
N.B. Les tables ne donnent que les valeurs de . Vous pouvez facilement en déduire  et k.
2.4. Remarques.
2.4.1. Dilatation d’une pièce creuse.
On pourrait montrer qu’un solide creux se dilate de la même façon qu’un solide plein de
même volume et de même nature. En particulier si l’on chauffe, une pièce le volume de la
partie creuse augmente et si on refroidit il diminue.
2.4.2. Masse volumique et température.
V
m
. Lorsque la température varie, le volume varie, la masse n’étant pas modifiée. La masse
volumique varie donc : elle diminue lorsque la température augmente et augmente lorsque la
température diminue.
 V
m
,
).k 1(V m
r
soit
θ)k. (1 ρ
ρr
θΔ
, en particulier
θ)k. (1 ρ
ρ0
θ
.
2.5. Applications.
Jeu de dilatation.
Bâtiment : les joints de dilatation sont protégés
par un remplissage souple.
Galets de roulement des ponts métalliques.
Joint de dilatation des rails.
Lyre de dilatation.
Coude en forme de lyre (instrument de musique)
pour les tuyauteries transportant des fluides à température élevée.
Frettage.
On place un cerclage à chaud sur une pièce froide.
Bilames.
Deux métaux ont des coefficients de dilatation différents.
 Sécurité pour le gaz.
 Disjoncteur thermique.
 Thermostat.
Contraintes de dilatation.
Si l’on empêche la dilatation d’un solide ou d’un liquide de se faire normalement à la pression
ordinaire, il va se développer dans le matériau des contraintes énormes.
gaz
Sécurité gaz
Lyre de dilatation
Galets

5
Il faut alors tenir compte, du coefficient de compressibilité du corps afin de calculer la
pression nécessaire pour qu’il conserve son volume initial à la température de l’expérience, ou
du module d’Young pour qu’il conserve sa longueur initiale.
Formule de Hooke.
Considérons une barre de section S et de longueur L maintenue à température constante. Si on
veut l’allonger de la quantité L, la loi de Hooke indique qu’il faut exercer la force de traction
F
telle que
L
L
.E
S
F
(figure 1).
La constante E, caractéristique du matériau est le module d’Young ; il s’exprime en N.m-2 (ou
Pa) et vaut, pour l’acier par exemple, environ 21011 Pa.
Si vous décidez de ramener à sa longueur initiale la barre, il vous faudra exercer la force de
compression
'F
opposée à
F
, donc de même valeur F.
Si enfin une butée vient contrarier l’allongement d’une pièce qui s’allongerait de L sans
contrainte, sous l’effet d’une augmentation de température  par exemple, cette butée
exercera sur la pièce une force égale à
'F
, de valeur F telle que
L
ΔL
E
S
F
.
Coefficient de compressibilité.
Les tables donnent les valeurs des coefficients de compressibilité
P
V
V
1
de différents
matériaux, à la température de 20°C.
Corps
Limites de pression (bar)
 (en bar1)
Eau
0 à 500
42,0  106
Fer
1 et au-dessus
0,60106
Cuivre
0,76106
Aluminium
1,38106
1 bar = 105 Pa 1 Pa = 1 N.m-2
Ces valeurs faibles, les solides sont très peu compressibles, varient relativement peu si
l’élévation de température est modérée.
Par un raisonnement analogue au précédent, tout blocage d’une augmentation de volume V
liée à une augmentation de température  s’accompagnera de l’augmentation de pression
V
V
1
P 
.
3. Dilatation des liquides.
Les liquides se dilatent… mais les récipients qui les contiennent aussi : on est amené à définir 2
coefficients de dilatation.
'F
x
L
0
Section S (m2)
F
x
L (L  L)
0
Section S (m2)