HIGH-TECH ANNEE : 2009/2010

HIGH-TECH ANNEE : 2009/2010
-Pr : M.EL MOUEDEN- - Cours : Antennes - Page 1
C
CH HA AP PI IT TR RE E I II I
D
DE EF FI IN NI IT TI IO ON NS S E ET T P PR RO OP PR RI IE ET TE ES S
C
CA AR RA AC CT TE ER RI IS ST TI IQ QU UE ES S
D DE ES S A AN NT TE EN NN NE ES S
L
LE ES S A AN NT TE EN NN NE ES S

HIGH-TECH ANNEE : 2009/2010
-Pr : M.EL MOUEDEN- - Cours : Antennes - Page 2
SOMMAIRE
– Introduction.
– Paramètres caractéristiques d’une antenne.
 Puissance,
 Directivité,
 Gain,
 Surface équivalente à une antenne.
 Impédances…
– Paramètres particuliers.
– Application à l’équation des télécommunications.
– Théorème de réciprocité.

HIGH-TECH ANNEE : 2009/2010
-Pr : M.EL MOUEDEN- - Cours : Antennes - Page 3
– Introduction.
En émission, certaines antennes peuvent être modélisées
par la distribution des courants qui interviennent dans la
répartition de l’énergie rayonnée dans l’espace.
Pour d’autres antennes, le champ rayonné est calculée à
partir de sa distribution sur une surface en utilisant la
formule de Kirchoff ou sur une surface équivalente.
D’une façon générale, on est amené à considérer un
certain nombre de paramètres communs à toutes les
antennes, et qui caractérisent le rayonnement.
Par ailleurs, l’antenne ne crée pas de l’énergie qu’elle
rayonne, mais elle assure la transformation de l’onde guidée
depuis l’émetteur en une onde susceptible de se propager en
l’espace libre.
Cette transformation doit se faire avec le meilleur
rendement énergétique. On voit alors apparaître un problème
d’adaptation et de définition d’impédance de l’antenne par
rapport à son point d’alimentation.
Sur le plan de la réception, l’antenne est le siège d’une
répartition d’une énergie différente de celle de l’émission.
Elle se comporte comme un générateur pour le récepteur
auquel elle est reliée, présentant toujours à son point
d’alimentation la même impédance. Celle-ci ne dépend que
de la nature physique et géométrique de l’antenne.
Les caractéristiques de l’antenne à la réception peuvent
de déduire facilement de celles de l’émission en utilisant le
théorème de réciprocité.

HIGH-TECH ANNEE : 2009/2010
-Pr : M.EL MOUEDEN- - Cours : Antennes - Page 4
- Paramètres caractéristiques d’une antenne.
- Densité de puissance par unité d’angle solide
 Antenne de référence : la source isotrope.
La source isotrope est constituée par une source
ponctuelle qui rayonne sa puissance d’alimentation Pa de
façon identique dans toutes les directions.
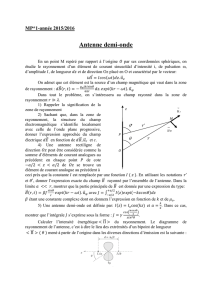
Dans un milieu homogène et isotrope, l’onde rayonnée
est une onde sphérique c'est-à-dire que les surfaces
équiphases sont des sphères centrées sur cette source
(figure1).
Bien qu’une telle source, ponctuelle et
omnidirectionnelle, n’ait pas de réalité physique dans le
domaine des ondes radioélectrique, elle est très utilisée
comme source de référence.
o
z
y
x
P’
θ
φ
R
P
Δ
Définition d’un point P et d’une
direction Δ dans un système de
Figure 2
Source à rayonnement
omnidirectionnel. Puissance
rayonnée par unité d’angle solide
Figure 1
R2
1 St

HIGH-TECH ANNEE : 2009/2010
-Pr : M.EL MOUEDEN- - Cours : Antennes - Page 5
La puissance rayonnée par unité d’angle solide (l'angle solide,
dans l'espace tridimensionnel, est défini comme le rapport de la surface d'une partie
d'une sphère sur le rayon au carré. Son unité est le stéradian noté sr. Pour calculer
l'angle solide sous lequel on voit un objet à partir d'un point donné, on projette l'objet
sur une sphère de rayon R centrée en ce point. Si la surface que cette projection fait
sur la sphère est S, l'angle solide sous lequel l'observateur voit l'objet est, par
définition : Ω=S/R2) dans une direction quelconque Δ définie par
une sphère : Pa :
Cette puissance rayonnée est
appelée aussi intensité de
rayonnement exprimée en
watts/stéradian.
La puissance rayonnée par unité de surface à la distance
R, ou densité de puissance est : puisque la surface de
R2.
On notera cette puissance p, telle que:
Le
c
co on nc ce ep pt t d de e p pu ui is ss sa an nc ce e r ra ay yo on nn né ée e p pa ar r u un ni it té é d d’ ’a an ng gl le e
s
so ol li id de e
est intéressant parce qu’elle
n
ne e f fa ai it t p pa as s i in nt te er rv ve en ni ir r l la a
d
di is st ta an nc ce e à à l la aq qu ue el ll le e o on n s se e p pl la ac ce e
. Il est donc plus général que
celui de la puissance rayonnée par unité de surface. C’et pour
cette raison qu’on la définie par : puissance rayonnée par
unité d’angle solide.
En pratique, on mesurera en un point de l’espace :
- Soit la puissance rayonnée par unité de surface : la
mesure s’effectue à l’aide d’un wattmètre ;
- Soit le champ rayonné, et il s’agira alors du champ
électrique (V/m) : la mesure s’effectuera dans ce cas à
l’aide d’un champmètre.
Rappel : la puissance par unité de surface (dite aussi densité
de puissance ) est aussi donnée par le vecteur de Poynting :
(Watts)
Pa
p=
1
E Λ H*
1
2
Pa
2
(W/m2)
Pa
2