chap2

1
Chapitre II : Applications de la plasticité
Matériaux élasto-plastiques à paramètres structuraux
Matériaux viscoplastiques

2

3
I. Matériaux élastoplastiques à microstruces variant avec la
déformation
I.1. Matériau élastoplastique poreux
Considérons un matériau élastoplastique contenant une fraction volumique f de
cavités sphériques.Ces cavités peuvent venir de l'élaboration (compaction incomplète) ou
apparaître pendant la déformation autour de particules de secondes phases due à une rupture
de l'interface inclusion matrice.La matrice a un comportement élastoplastique écrousissable
décrit par
M
n
M
p
00
1
00
E
où M est la contrainte d'écoulement de la matrice et
M
pM
pdt
est la déformation
équivalente de von Mises dans la matrice.
0
et
0
sont deux constantes caractéristiques du
comportement de la matrice. E est le module de Young de la matrice.
Nous voudrons connaître la relation entre les contraintes macroscopiques  et
déformations macroscopiques  décrivant le comportement de l'ensemble matrice et cavités.
M
n
M
p
00
1
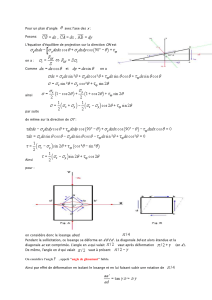
f=f0+df
- a - -b-
Figure 1 : microstrure du composite matrice-cavités (a) avant déformation, (b) apès déformation
Pendant la déformation la fraction volumique de cavités et leur forme change. Nous
supposerons pour le moment que les cavités restent sphériques. Ceci permettra de caractériser
la microstructure du matériau par un seul paramètre scalaire : la fraction volumique de cavités.

4
I.1.1. Potentiel des contraintes de Gurson
Gurson a estimé le champ de vitesse et de déformation dans une sphère creuse
soumise sur la surface externe à un chargement imposé. Basé sur les résultats de Gurson, le
potentiel suivant semble bien décrire le comportement d'un matériau élasto-plastique
contenant des cavités sphériques. Les facteurs q1 et q2 ont été introduit par Tvergaard afin de
rendre compte de résultats obtenus par éléments finis.
eq
M
m
M
qfqqf
2
1 2 2
1
23
21 0
cosh
Les vitesses de déformation plastiques sont définies comme au préalables par la loi de
normalité :
ij
p
ij
E
eq
et
m
sont respectivement la contrainte de von Mises et la contrainte moyenne
macroscopique
eq ij mij m m kk
3
21 3
Le potentiel des contraintes dépend de la contrainte moyenne macroscopique puisque
l'accroissement de volume dû à la déformation plastique est non nul ici. En effet, pendant la
déformation du composite, la matrice se déforme de façon incompressible, mais le volume des
cavités peut varier.
I.1.2 Tenseur vitesse de déformation plastique, loi de normalité
Exactement comme pour un matériau isotrope incompressible, les vitesses de
déformation plastiques sont données par la loi de normalité. Or maintenant, la normale à la
surface d'écoulement ou au potentiel des contraintes a une composante non nulle suivant la
direction de la contrainte moyenne :
ij
p
ij ij ij m
ES
1
3
où est le facteur indéterminé et S le tenseur déviateur macroscopiques des contraintes. La
contrainte m est indépendante des composantes du tenseur déviateur. Donc la dérivée par
rapport à S dans le premier terme du membre de droite peut ête calculée par une dérivation par
partie par rapport à eq :

5
ij
p
eq
ij
eq ij m
ES
3
21 3
3
2eq eq
est un scalaire et S est à trace nulle (Skk=0). Donc le premier terme dans le
membre de droite est à trace nulle. C'est le terme classique retrouvé dans le cas d'un matériau
isotrope incompressible. Ainsi le déviateur des vitesses de déformation plastiques s'écrit :
ij
p
eq
ij
eq
ES
'
3
2
Et la vitesse de déformation équivalente de von Mises est définie comme précédemment :
p
eq
ikk
p
m
E
La trace des vitesses de déformation plastiques équivaut à l'accroissement de volume
du composite pendant la déformation plastique et s'écrit :
kk
p
m
V
VE
Nous spécifions maintenant les différents termes intervenant dans la vitesse de
déformation plastique
eq
eq
M
22
mM
h
M
q q fq
2 3
23 2
1 2 2
sinh
Introduisant le paramètre l défini comme suit :
1
23 2
1 2
qfqh
M
sinh 
Ainsi la vitesse de déformation peut s'écrire
ij
peq
M
ij
eq ij M
m
M
ESq q fq
sinh( ) 
23
21 32 3 23 2
21 2 2
soit
ij
p
M
ij
Mij
ESq
2 3
22