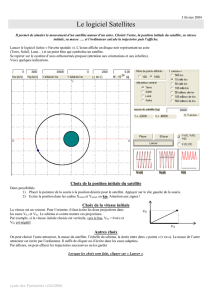
P11 (2) Mouvement des satellites artificiels de la Terre.

Lycée Jean XXIII REIMS
Chapitre P11 – Fiche TP Terminale S
1/2
ETUDE DU MOUVEMENT DES SATELLITES DE LA TERRE
Objectif - Vérification qualitative des lois de Kepler.
- Conditions d’obtention du mouvement circulaire uniforme d’un satellite autour de l’astre attracteur.
Activité préparatoire
Le programme de TS se limite au cas des satellites en mouvement circulaire et uniforme autour d'un astre attracteur.
Quel référentiel galiléen allez vous utiliser pour l'étude du mouvement des satellites autour de la Terre?
Soit m la masse du satellite et MT la masse de la Terre, établir :
- en utilisant le théorème du centre d'inertie,
- en considérant que la seule force qui s'exerce est la force gravitationnelle de la Terre,
que si le mouvement du satellite est circulaire de centre l'astre attracteur alors le mouvement est forcément circulaire et
uniforme
En déduire :
- La relation entre la vitesse du satellite en MCU et le rayon de la trajectoire R.
- La relation entre la période T du MCU du satellite et la valeur de R.
- L’expression du rapport
3
2
R
T
. Ce rapport dépend t-il de la masse du satellite?
I) Condition d'obtention d'un mouvement circulaire uniforme (MCU) du satellite autour de l'astre
attracteur
1) Le plan de l'orbite d'un satellite
On admettra que les satellites tournent autour de l'astre attracteur sur une orbite plane qui contient le centre de l'astre
attracteur. La modélisation se fait donc vue du dessus du plan de l'orbite et la feuille de papier ou l'écran est le plan de
l'orbite. Les orbites les plus stables sont celles situées dans un plan voisin de l'équateur.
2) Cas du mouvement de la Lune autour de la Terre : simulation à l’aide du logiciel Dynamic en ne
considérant que l'attraction gravitationnelle de la Terre
Observation de la simulation
Dans Dynamic : Fichier>Ouvrir>Lune, lancer la simulation : Trajectoire>Tracé.
Quelle est la forme de la trajectoire ?
Quelle est la valeur de la vitesse dont on trace des vecteurs sur la trajectoire ?
Quelle est la particularité du vecteur accélération ?
On peut arrêter le tracé définitivement on cliquant sur Fin ou temporairement on cliquant sur Stopper.
Paramètres :
Distance centre de la Terre centre de la Lune ou rayon de la trajectoire DT-L=………………
Masse de la Terre: MT =………………
Masse de la Lune: m=………………
Rayon de la Terre RT =………………
Période TL de rotation de la Lune autour de la Terre en secondes et en jours = ………………
Remarque
En réalité la Lune décrit une ellipse et sa période de révolution est de29j et 12h.
Aide pour tracer quelques vecteurs vitesse et accélération et lire leur valeur en haut à gauche de l'écran :
Clic gauche sur (vitesse),
clic gauche sur point de la trajectoire où on veut tracer le vecteur vitesse,
sa valeur s'affiche en haut à gauche.
3) Etude dynamique de la Lune en supposant le mouvement circulaire et uniforme
Quel référentiel galiléen allez vous utiliser ?
Dans quel repère allez vous travailler ?
Déduire de votre étude l'expression littérale de la vitesse (v) du mouvement circulaire uniforme de rayon DT-L en
fonction des paramètres indiqués sur la simulation.
Cette valeur de v dépend t-elle de la masse de la Lune ?
Vérifier numériquement que vous trouvez à peu près la même valeur de v que celle indiquée par le logiciel (en fait
1023 m/s).
Vérifier la validité de votre modèle en changeant la masse de la Lune.
Donner par exemple la valeur 1kg à la Lune : Initialiser>Paramètres>Fiche masse taper 1,00 kg.
ATTENTION : Taper une virgule et non un point sinon la modification n'est pas prise en compte

Lycée Jean XXIII REIMS
Chapitre P11 – Fiche TP Terminale S
2/2
Relancer un nouveau tracé en changeant au préalable la couleur du tracé : Clic gauche (CG) sur la palette de couleurs
dans la barre d'outils Dessin à gauche.
Donner l'expression de TL: période du MCU de la Lune autour de la Terre en fonction de sa vitesse v et du rayon de
l'orbite DT-L.
Faire l'application numérique : on doit retrouver l'ordre de grandeur de la valeur proposée
4) Variation de la trajectoire du satellite autour de la Terre en fonction de la valeur de la vitesse initiale
du satellite
Effacer vos travaux et réinitialiser les paramètres en rouvrant le fichier Lune.
Modification de la valeur de la vitesse initiale perpendiculaire à la force
Initialiser >Vitesse>Modifier> Fiche vx (conserver la valeur) : OK> Fiche vy (modifier la valeur)
Pour chaque valeur de vy, tracer les trajectoires et observer :
o vy =100 m/s.
o vy =500 m/s en changeant dt=100s pour minimiser les divergences de calcul du logiciel (initialiser>
paramètres>fiche dt: taper 100s).
o vy =900m/s et dt = 400s.
o vy =1200m/s et dt=500s.
Conclusion générale
La trajectoire d'un satellite en orbite est une ellipse dont l'astre attracteur occupe un des foyers (première loi de
Kepler)
Pour une certaine valeur vMCU de la vitesse initiale perpendiculaire à la force gravitationnelle le satellite a un mouvement
circulaire uniforme de rayon R :
Pour v >vMCU la trajectoire est ……………………………..de ½ grand axe ……………….……que R
Pour v<vMCU la trajectoire est……………………………...de ½ grand axe………………………que R
Si V est cependant trop faible voire nulle le solide tombe sur la Terre.
Lorsque la trajectoire est une ellipse :
Plus le satellite est proche de l'astre attracteur, plus sa vitesse est …………………
Plus le satellite est loin de l'astre attracteur, plus sa vitesse est………………….
Des calculs de surface montreraient que Le rayon Astre attracteur -- Satellite balaie des surfaces égales pendant des
durées égales (2ème loi de Kepler).
II) Cas du satellite géostationnaire
1) Définition
Un satellite géostationnaire est un satellite en mouvement circulaire uniforme autour de la Terre qui tourne dans le même
sens que la Terre avec la même période. Ce satellite reste donc toujours à la verticale d'un même lieu.
Cette période de rotation de la Terre sur elle même est appelée le jour sidéral : 1 jour sidéral = 86140s.
Remarque
La durée de 24 h =86400 s correspond au jour solaire: durée qui sépare deux passages consécutifs du soleil à la verticale d'un
lieu. La différence entre jour solaire et sidéral vient du fait que la Terre tourne sur elle même mais aussi autour du soleil.
Les satellites de télécommunication pour la réception de la télévision sont ils géostationnaires? Justifier-le sans calcul.
2) Relation entre période de révolution T d'un satellite de la Terre en MCU et rayon de sa trajectoire R
Démonstration de la troisième loi de Kepler
A l'aide des relations trouvées au I) exprimer cette relation qui est en fait la 3ème loi de Kepler.
Application
Donner la valeur du rayon R de la trajectoire d'un satellite géostationnaire et la valeur de son altitude.
3) Relation entre vitesse v d'un satellite en MCU et le rayon R de sa trajectoire
Comment évalue v en fonction de R ?
4) Visualiser la simulation et vérifier vos résultats en ouvrant le fichier météosat.dat.
1
/
2
100%