Mécanique NYA Notes de cours

Mécanique NYA Notes de cours
Thèmes : Travail, énergie et puissance
Introduction
Les notions, comme le travail et l’énergie, qui seront vues dans cette section
étaient inconnues de Newton mais découlent en fait, comme nous le verrons,
de ce que nous avons déjà vu. Nous commencerons d’abord par des
définitions reliées au travail dont nous envisagerons d’abord le mode
d’application. Ensuite nous nous rattacherons à la 2ième loi de Newton à
travers le théorème sur l’énergie cinétique qui sera en quelque sorte au cœur
de notre exposé. Finalement les forces conservatives, pour lesquelles on peut
parler d’énergie potentielle et les autres forces, non conservatives, amènent à
un déploiement plus raffiné du théorème sur l’énergie cinétique. De
nombreux exemples avec conservation ou non conservation de l’énergie
mécanique sont considérés. Nous allons boucler cette section par la notion
de puissance et divers compléments.
a) Le produit scalaire
Commençons par définir et développer un outil mathématique qui nous sera
utile à savoir le produit scalaire.
A
B
(Les origines des vecteurs
coïncident dans la considération de l’angle.)
cosBABA  
Grandeurs
Notation d’un
produit scalaire

2
Le produit reçoit son nom du fait que le résultat correspond ici à un scalaire.
Plus tard, nous verrons par contre le produit vectoriel.
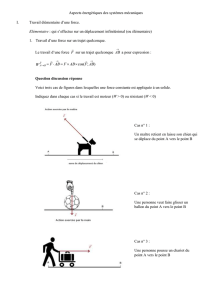
Divers cas possibles
N.B. Bien retenir que pour deux vecteurs perpendiculaires l’un à l’autre, leur
produit scalaire est nul.
 Propriétés du produit scalaire
- Commutatif :
ABBA 
- Distributif :
CABACBA 
 Développement du produit scalaire à partir des composantes
Il est souvent utile de développer un produit scalaire à partir des
composantes de deux vecteurs.
0 BA 
0 BA 
0BA 
A
A
A
B
B
B
x
y
A
B
i
j

3
Appliquons notre définition du produit scalaire aux vecteurs unitaires
i
et
j
:
0 ijji 
(les vecteurs sont perpendiculaires l’un à l’autre)
10cos110cos  jiii 
et
1 jj 
Nous pouvons maintenant développer l’expression recherchée :
jBiBjAiABA yxyx
En appliquant tout ce que nous avons vu, nous obtenons aisément :
yyxx BABABA  
En trois dimensions s’ajoute un terme supplémentaire évident.
Un cas particulier intéressant est le suivant :
Pythagore de théorème0cos 222 yx AAAAAAA  
Application
Retrouver la loi des cosinus.
'cos2
cos22
222
22222
BABAC
BABABABABABACCC
A
B
C
'

4
b) Travail fait par une force constante
Considérons la situation suivante où une force constante
F
opère sur un
objet pendant que celui-ci effectue un déplacement
s
:
Le travail fait par la force
F
se calcule de la façon suivante :
cossFsFWF 
Unités
1 J (joule) = 1 N∙m
c) Travail fait par une force variable en une dimension
Pour bien saisir le principe que nous allons appliquer, nous commencerons
par considérer le cas d’une force constante :
Nous avons :
iFF x
et
ixxs if
. Le travail peut être facilement
évalué :
ifx xxFsF  
N.B. D’autres forces seront généralement
présentes.
s
F
x
s
F
i
x
f
x
0

5
Ce résultat peut être interprété graphiquement :
C’est ce même principe que nous appliquerons pour une force variable :
Cas d’un ressort
C’est le principal cas que nous allons considérer. Nous supposerons ici que
nos ressorts obéissent à la loi de Hooke qui est généralement valable si
l’élongation ou la compression du ressort n’est pas trop grande :
xkFr
x
x
F
Le travail correspond à l’aire « sous la
courbe ».
i
x
f
x
0
x
F
x
i
x
f
x
0
f
i
x
xxdxF Aire