Distance de freinage

Distance de freinage
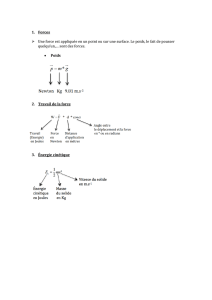
Tout objet en mouvement cumule de l’énergie appelée énergie cinétique ; Lorsque la vitesse
augmente, l’énergie cinétique augmente également…
Pour arrêter un objet en mouvement, il faut que son énergie cinétique devienne nulle : c’est le freinage,
qui prend du temps et nécessite une certaine distance, la distance de freinage.
1. Pour des raisons pratiques, il est plus commode d’utiliser comme unité de vitesse le m.s-1 (mètre par
seconde) plutôt que le km.h-1.
a. Calculer la distance en km parcourue en 1 heure par un objet qui se déplace à 1 m.s-1.
b. En déduire la valeur de 1 m.s-1 exprimée en km.h-1.
(Noter les réponses dans une cellule de la feuille de calcul)
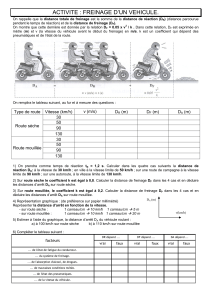
2. Soit v la vitesse d’un véhicule en m.s-1 ; la distance de freinage dF de ce véhicule est donnée par la
fonction dF : v kv² (k est un coefficient qui dépend de l’état de la route).
1° cas : Dans des conditions « normales », lorsque la route est sèche, le coefficient k est égal à 0,08.
Calculer pour chacune des vitesses v du tableau ci-dessous la distance de freinage dF.
a) Recopie le tableau suivant sur la feuille de calcul du logiciel pour une vitesse variant de 0 à 40 m.s-1
(pas de 2,5)
b) Pour compléter ce tableau de valeurs :
Dans la case B2 :
– taper le signe « = » qui indique que l’on va entrer une formule
– taper la formule « 0,08*B1*B1 »
– valider en tapant sur « entrée »
– Sélectionner par un clic gauche la celluleB2 et positionner le curseur dans le coin inférieur droit.
– Le curseur prend alors la forme d’une croix que l’in tire vers la droite en maintenant appuyé le
bouton de la souris
–
c) Pour représenter la fonction graphiquement dF
- Sélectionner les lignes 1 et 2 et ouvrir l’assistant graphique en cliquant sur
- sélectionner XY dispersion (ou nuage de points), cocher lignes lisses et choisir points et
et lignes
- cliquer suivant et choisir séries de données en ligne puis terminer la construction (étape 4 cocher
x et y)
Il est souvent nécessaire de modifier les unités des axes :
- sélectionner l’axe et à l’aide du clic droit, sélectionner « formater l’axe » afin de changer l’échelle
d) En utilisant ce graphique, déterminer une valeur approchée de :
- la distance de freinage lorsqu’on roule à 28 m/s
- la vitesse correspondant à une distance de freinage de 25 m
(Noter les réponses dans une cellule de la feuille de calcul)
d) Rajouter une ligne au tableau en utilisant « insertion » « lignes » pour donner la vitesse en km/h
correspondante
2° cas : Lorsque la route est mouillée, en cas de pluie, le coefficient k est égal à 0,14. Reprendre
l’exercice précédent avec cette nouvelle valeur du coefficient k sur l’onglet « feuille 2 » qui se
trouve en bas de la page.

DM 7
(Suite de l’activité distance de freinage faite en classe)
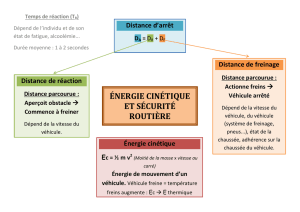
Pour arrêter un objet en mouvement, il faut que son énergie cinétique devienne nulle : c’est le
freinage, qui prend du temps et nécessite une certaine distance, la distance de freinage.
Mais, le conducteur a aussi besoin d’un temps de réaction pour identifier la situation, prendre
une décision adéquate (décider de freiner) et répondre efficacement (freiner). On estime que dans
des conditions psychologiques et physiologiques normales, ce temps de réaction oscille entre 0,6
seconde et 2 secondes.
Entre le moment où le conducteur identifie la situation et commence effectivement à freiner, il a
donc parcouru une certaine distance, appelée « distance de réaction ».
En notant dA la distance d’arrêt et dR la distance de réaction, on a donc : dA = dR + dF.
On choisira pour la suite le temps de réaction (minimum) de 0,6 seconde.
Fin du travail sur tableur : Rajouter deux lignes aux tableaux précédents pour obtenir les tableaux
suivants sur route sèche mais aussi sur route mouillée
Utilisation des calculs du tableur :
. Alex roule en scooter, en ville, à une vitesse de 36 km.h-1.
a. Convertir cette vitesse en m.s-1.
b. À l’aide des tableaux, donner la distance de freinage du scooter sur route sèche, puis sur route
mouillée.
c. Donner la distance d’arrêt sur route sèche puis sur route mouillée.
d. Sur la route qu’a empruntée Alex, un enfant surgit brusquement ; au moment où Alex
commence à freiner (ne pas tenir compte du temps de réaction), l’enfant est à 9 m de lui. Y a-t-
il un risque de collision ? Comment doit-on adapter sa vitesse ? Expliquer la réponse.
e. Déterminer par le calcul la vitesse maximale à laquelle Alex aurait dû rouler sur la route mouillée
pour éviter l’accident. On donnera d’abord une valeur approchée au dixième en m.s-1, puis une
valeur approchée à l’unité en km.h-1.
Noter les réponses aux questions posées sur la feuille de calcul, veiller à soigner la
présentation, enregistrer le travail et l’envoyer par mail à l’adresse suivante :
[e-mail]