le lien vers le compte rendu de notre expérience

Expérience de logistique
Nous savons que plusieurs plans existent afin de repérer les géocroiseurs en orbite
instable dans le système solaire. Maintenant, partant du principe que l’on connaît la distance,
la masse et la vitesse de l’astéroïde menaçant, nous allons essayer de reproduire une
simulation simplifiée de sa trajectoire à venir.
Notre objectif est donc de déterminer la trajectoire et ses probabilités de collision avec
la Terre d’un astéroïde imaginaire. Nous ferons évoluer l’expérience en fonction de son
positionnement par rapport à la Terre, sur la ceinture comprise entre Mars et Jupiter (à 450
millions de kilomètres du soleil).
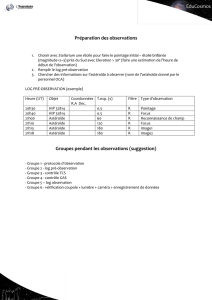
L’expérience est réalisée les 15/12/2005, 05/01/2006, 12/01/2006, 19/01/2006 de 8h00
à 10h00 dans une salle informatique de notre lycée. Clément s’occupe principalement de la
mise au point de la partie programmation de l’expérimentation tandis que Sylvain s’affaire à
l’interprétation des résultats.
Protocole expérimental :
Matériel nécessaire :
- 8 ordinateurs
- un logiciel de calcul de trajectoire (Astéroïde)*
- Un logiciel de modélisation graphique (Gnu plot).
- Un logiciel de modélisation par animation des trajectoires (AsTPEroide conçu par
Clément avec le langage informatique Python)*
1) Sur 8 ordinateurs différents, nommés P1, P2, P3, P4, P5, P6, P7, P8 correspondant à 8
angles téta différents (angle de dérivation entre l’orbite initiale de l’astéroïde –
circulaire autours du soleil - et sa nouvelle susceptible d’être géocroiseur) 0°, 20°,
40°, 60°, 80°, 100°, 120°, 140°, on pratique 8 calculs de trajectoires d’astéroïde
variant en fonction d’un angle alpha (angle initial par rapport à la Terre) égal à 0°, 30°,
60°, 120°, 180°, 240°, 300°, 330°. L’astéroïde se trouve à 450 millions de Km du
soleil (la Terre à 150) une masse de kg. Pourquoi ces angles ? Nous avons choisi de
couvrir tous les angles représentatifs des possibilités de trajectoires. Nous savons que
pour dévier l’astéroïde vers le système solaire interne, il faut un téta compris entre 0 et
180 degrés. Le alpha lui doit être testé sur 360°. En choisissant ces angles (0°, 20°,
40°, 60°, 80°, 100°, 120°, 140 pour le téta et 0°, 30°, 60°, 120°, 180°, 240°, 300°, 330°
pour le alpha) nous couvrons toutes les possibilités potentiellement intéressantes de
modélisation. Nous avons choisi d’étudier les angles 30 et 330 parce que l’on suspecte
les risques d’être plus grands quand la Terre est à proximité de l’astéroïde lors de la
déviation initiale.
On admet pour la Terre une masse de 5.976E24 Kg et le Soleil de 1.989E30 Kg.
Représentation des angles variés pour modifier le positionnement et la trajectoire de
l’astéroïde :

Afin de calculer la trajectoire de l’astéroïde dans le système solaire, le logiciel
Astéroïde utilise la formule suivante :
 F = m.a
Avec  F = FT/A + FS/A
a = dv/dt = v ’
Avec
m : masse de l’astéroïde (elle n’a pas beaucoup d’importance du fait qu’elle s’annule
de part et d’autre de l’équation)
v ’ : dérivée de la vitesse
Les résultats sont classés et enregistrés.
2) Les résultats, réunis alors sur un seul poste, sont analysés très rapidement avec le
logiciel Gnu plot qui nous présente un graphique avec les trajectoires ou les distances
séparant l’astéroïde de la Terre. Cette manipulation permet de vérifier qu’il n’y a pas
eu d’erreurs de manipulation mais aussi de retenir seulement les astéroïdes les plus
intéressants, c’est à dire les géocroiseurs susceptibles d’entrer en collision avec la
Terre.
3) Les courbes de géocroiseurs sont alors modélisées sur notre logiciel d’animation en
python. Dès lors on peut constater si oui ou non l’astéroïde passe près de la Terre.
Avant de traiter de nos résultats, il est important de préciser que le dimanche 15
janvier 2006 ont été détectées de nombreuses erreurs du fait d’une confusion entre l’angle
alpha et téta dans les calculs de trajectoire exécutés le 15/12/2005. Ceux-ci ont donc été
rectifiés le jeudi suivant, le 19/01/2006.
Aucune autre erreur de manipulation n’a été détectée à ce jour.

Le seul type d’erreur possible est donc celui de l’imprécision des logiciels qui parfois
finissent par aboutir sur un résultat aux limites de la logique, notamment pour les courbes
avec un angle téta compris entre 80° et 100°.
Nb : afin de prévoir le bon fonctionnement de notre logiciel de modélisation animée
en Python, l’écran doit être reconfiguré en 1024X768 au minimum.
Résultats et interprétation.
Dans notre première vague de calculs peu ciblés (pris le 15/12/2005 et le 05/01/2006),
on ne dénote aucune collision. Pour certains astéroïdes, même s’ils sont présents dans les 20
années qui viennent, le risque d’une rencontre avec la Terre reste très faible puisque
l’astéroïde au plus proche se limite à 1 million de km. C’est sans compter avec le fait que
l’attraction terrestre influe peu comparée à la dominance de celle du Soleil.
C’est plus tard que nous avons véritablement approfondi nos recherches. Pour suivre
l’exploitation complète des résultats, reportez vous à la partie II du dossier.