I- Buts

Oscillations libres amorties
I/ But de la manipulation :
-réaliser un montage permettant de suivre les oscillations libres d’un circuit RLC série.
-reconnaitre le régime pseudopériodique et le régime apériodique ainsi que le facteur responsable de
l’amortissement.
-Etablir l’équation différentielle régissant les oscillations libres amorties d’un circuit RLC série.
-Interpréter la diminution de l’amplitude des oscillations libres amorties par le transfert d’énergie de
l’oscillateur vers l’extérieur.
II/Manipulation :
1°/Circuit électrique :
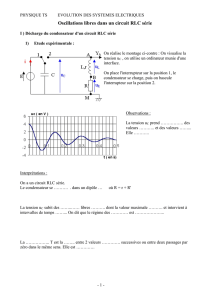
Réalise le circuit électrique schématisé ci-contre ou
C=0,5µF ; L=1H ; r=15Ω et R=100Ω.
Remarque :
La charge et la décharge du condensateur sont extrêmement
rapides. L’utilisation d’un oscilloscope à mémoire permet de
visualiser les tensions uC et uR. A défaut d’un tel oscilloscope,
on utilise un générateur délivrant une tension carrée qui assure
une série de charge et de décharge du condensateur.
2°/Production des oscillations électriques :
-Le commutateur K est dans la position 1 :
Le condensateur se charge. La tension uC aux bornes du condensateur est égale à celle aux
bornes du générateur.
-Le commutateur K est dans la position 2 :
Le condensateur se décharge dans le dipôle RL. Cette décharge
est oscillante a cause de la bobine. Le circuit RLC série constitue un système oscillateur.
Le circuit RLC série fermé, avec le condensateur initialement chargé peut être le siège
d’oscillations électriques amorties. De telles oscillations qui s’effectuent d’elles mêmes sans
l’intervention d’un agent extérieure sont dites libres. Ces oscillations libres amorties sont
pseudopériodiques de pseudo période T.
La résistance totale du circuit est le facteur responsable de l’amortissement.
3°/ Influence de l’amortissement :
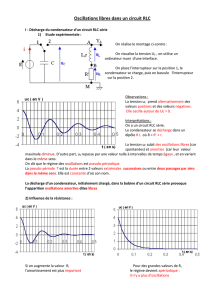
Faire varier R de 100Ω à 5kΩ et observer :
-Représenter la courbe de variation de uC(t) et la courbe de variation de uR(t) suivant
l’importance de R.
Le circuit RLC série fermé, avec le condensateur initialement chargé, ne peut osciller que
lorsque l’amortissement est faible. Plus la résistance du circuit est élevée, plus la pseudo
période est grande et plus le retour de l’oscillateur à son état d’équilibre est rapide. Pour des
valeurs élevées de R, le régime n’est plus oscillatoire, il est apériodique.
4°/Equation différentielle régissant l’évolution d’un circuit RLC série en régime libre :
D’après la loi des mailles, uR + uB +uC=0.
dt
dq
iavec
C
q
iriR
dt
di
L ;0...
0).(
2
2
 C
q
dt
dq
rR
dtqd
L
5°/Energie totale d’un oscillateur RLC série :
a-A l’aide d’un logiciel on calcule :
- L’énergie électrique Ec=
1
2
Cu
2
C
- L’énergie magnétique EL=
1
2
Li2 =
1
2
L(
2
2
R
u
R
)
b-Représenter la courbe associée à l’énergie totale du circuit E = Ec + EL
c-Justifier la non conservation de l’énergie totale d’un circuit RLC série.
Voie B
uC
R
i
Voie
A
M
G
K
2
1
C
L, r

E=
0).().(.....
2
1
.
212
2
2
22  irR
dtqd
L
C
q
i
dt
di
iL
dt
dq
C
q
dt
dE
iLq
C
L’énergie du système
oscillateur est dissipée sous forme de chaleur par effet joule par la résistance totale du circuit.
Les courbes :
E=6V ; R=100 ; C=0,5µF ; L=1H
E=6V ; R=1000 ; C=0,5µF ; L=1H
E=6V ; R=5000 ; C=0,5µF ; L=1H

E=6V ; R=100 ; C=0,5µF ; L=1H
E=6V ; R=5000 ; C=0,5µF ; L=1H