Univers, Galaxies

Phys. N° 01 : L'Univers : de l'Atome aux Galaxies
OBJECTIFS :
Univers, Galaxies, …
Matière lacunaire.
Positionner des objets sur une échelle.
Conversion d’unité, puissance de dix, écriture scientifique.
Précision, chiffres significatifs.
Mesurer des distances
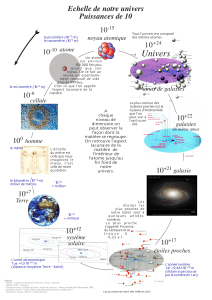
I- Présentation de l’Univers.
Vidéo « Puissances de dix »
1) L’infiniment grand.
Depuis l ‘Antiquité, les hommes ont observé le ciel. Ils se sont intéressés aux Etoiles, aux Planètes.
a) Le système Solaire :
Le Soleil et l’ensemble des objets en révolution autour de lui constituent le système Solaire.
La Terre fait partie du système Solaire avec huit autres planètes qui sont : Mercure, Vénus, la Terre, Mars,
Jupiter, Saturne, Uranus, Neptune, Pluton.
La Terre tourne autour du Soleil sur une orbite quasi circulaire de 150 millions de kilomètres de rayon. Cette
distance est appelée unité astronomique, notée UA. 1 UA = 1,5 x 10 11 m.
Les planètes et leurs satellites, les astéroïdes, les comètes font partie du système Solaire.
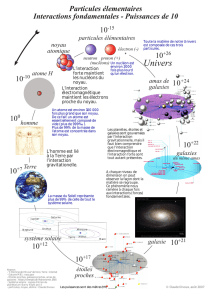
b) Notre Galaxie :
Toutes les étoiles que nous voyons à l’œil nu font partie de notre Galaxie.
Elle comporte environ 200 milliards d’étoiles. Elle a la forme d’un disque renflé au centre.
La bande lumineuse, d’apparence laiteuse que l’on observe dans le ciel, est notre Galaxie vue suivant un
diamètre de ce disque. On l’appelle la Voie Lactée.
Notre Galaxie s’étend sur 10 21 m. À cette échelle, le mètre et l’Unité Astronomique sont des unités mal
adaptés. On utilise l’année de lumière de symbole a.l.
1 a.l = 9,46 x 10 15 m
Exemple : Proxima du centaure est l’étoile la plus proche du Soleil. Elle est située à 40 mille milliards de
kilomètres. Cette grandeur s’exprime avec un nombre plus simple en utilisant l’année de lumière : 4,3 a.l.

c) L’Univers :
Il contient des milliards de Galaxies. La Galaxie d’Andromède, qui est la plus proche de la Terre, est située à
2 millions d’années de lumière. Les Galaxies sont regroupées en amas qui s’éloignent les uns des autres.
L’Univers est en expansion.
À l’aide des derniers télescopes, on peut observer l’Univers jusqu’à des distances de 15 milliards d’années
de lumière.
L’espace entre les étoiles et les Galaxies est surtout constitué de vide. À l’échelle cosmique, la matière est
essentiellement lacunaire.
2)- L’infiniment petit.
Les atomes : Ils peuvent être assimilés à des sphères dont le rayon atomique est de l’ordre de 0,1 nanomètre
(1 nm = 10 –9 m).
Un atome est constitué :
- D’un noyau central, chargé positivement
- Et d’électrons, chargés négativement en mouvement rapide autour du noyau.
Le noyau est assimilé à une sphère de rayon 100 000 fois plus petit que celui de l’atome. L’atome est
essentiellement fait de vide. Il a une structure lacunaire.
Les molécules : les plus petites molécules ont des dimensions de l’ordre du nanomètre. Certaines grosses
molécules organiques peuvent dépasser le millimètre (1 mm = 10 –3 m).
II- Des outils de description de l’Univers.
1) Les puissances de 10.
La notation scientifique :
a : nombre décimal compris entre 1 et 10 :
n : nombre entier positif ou négatif : .
Exemples :
Distance Terre – Soleil : 150 millions de kilomètres :
Taille d’une bactérie :
Formules :

2) Multiples et sous multiples d’une unité.
Facteur
multiplicatif
préfixe
Symbole
Etymologie
atto
a
Danois : atten : dix-huit
fento
f
Danois : femten : quinze
pico
p
Italien : picolo : petit
nano
n
Latin : nanus : nain
micro
Grec : mikros : petit
milli
m
Latin : mille : millième
unité
kilo
k
Grec : khilioi : mille
Méga
M
Grec : mégas : grand
Giga
G
Grec : gigas : géant
Téra
T
Grec : téras : monstre
Peta
P
Grec : pente : cinq (mille à la
puissance 5)
Exa
E
Grec : hex : six (mille à la puissance
6)
Exemples : le kilomètre : km ; le kilowatt : kW ; le millimètre : mm.
3) Ordre de grandeur.
L’ordre de grandeur d’un nombre très grand ou très petit est la puissance de 10 la plus proche de ce nombre.
Exemple 1 : L’atome de Germanium est représenté par une sphère de rayon Ra = 123 pm et son noyau a un
rayon Rn = 4,99 fm.
Donner un ordre de grandeur du rapport entre le rayon de l’atome et celui du noyau.
, en conséquence, le rayon de l’atome est
environ 20 mille fois plus grand que celui du noyau.
Combien d’atomes de Germanium faut-il aligner pour obtenir une longueur de 1 mm ?

Nombre d’atomes de Germanium nécessaires :il faut aligner 10
millions d’atomes de Germanium.
Exemples 2 :
Le nombre de secondes dans une année est-il de l’ordre : de la dizaine de milliards ? De la dizaine de
millions ? Ou de la dizaine de milliers ? Justifier la réponse.
, le nombre de secondes dans une année
est de l’ordre de la dizaine de millions.
4) Chiffres significatifs et précision d’une mesure.
Exemples : on donne la valeur du rayon de la Terre :
 Règle 1. dans l’écriture d’un nombre sous la forme , les chiffres utilisés pour
écrire le décimal a sont appelés chiffres significatifs.
Question : Combien de chiffres significatifs possèdent les grandeurs numériques (a), (b) et (c) ?
Pour répondre à la question, il faut utiliser la notation scientifique :
; cette expression possède 4 chiffres significatifs.
; cette expression possède 2 chiffres significatifs.
; cette expression possède 4 chiffres significatifs.
 Règle 2. Le nombre de chiffres significatifs utilisés pour exprimer une valeur donnée indique la
précision avec laquelle cette valeur est connue.
 Règle 3. On admet généralement que l’incertitude absolue, notée est égale à la demi-unité du
dernier chiffre significatif .
Explication :
1) Si on utilise la valeur suivante : ,
L’incertitude absolue sur cette mesure est : Ainsi, on peut
écrire: ou ou .
On a ou : INTERVALLE DE CONFIANCE
R - R < RT < R + R

2) Si on utilise la valeur :
L’incertitude
absolue est : ,
REMARQUE : Il est souvent commode de calculer l’incertitude relative donnée par la relation : . Cette
grandeur nous renseigne sur la précision de la mesure
1) : . On peut exprimer cette grandeur en pourcentage : .On dit que
la précision de la mesure est de : 0,78 %
2) : l’incertitude relative est : . La précision est de 0,0078 %
CONCLUSION : la valeur la plus précise est le (a).
 Règle 4. Le résultat d’une MULTIPLICATION (OU DIVISION) doit avoir le même nombre de chiffres
significatifs que la donnée qui en comporte le moins.
 Règle 5. Le résultat d’une ADDITION (OU SOUSTRACTION) doit avoir le même nombre de chiffres
après la virgule que la donnée qui en comporte le moins.
Exemple : Calculer la longueur de la circonférence de la Terre, sachant que , et
Longueur de la circonférence de la Terre :
On garde 3 chiffres significatifs et on arrondit (si le premier chiffre éliminé est supérieur ou égal à 5,
on majore d’une unité sinon on ne change rien).
Exemple : additionner 11,42 +2.345 puis 14,5 + 6,78
III) Mesure de distance à l’échelle humaine : TP1
Utiliser le bon instrument en fonction de la précision souhaitée (pied à coulisse, palmer, règle millimétrée,
décamètre, …).
IV) Mesure de petite distance, diamètre d’un cheveu : TP2
V) Mesure de grande distance, rayon de la Terre : ACTIVITE CDI, ERASTOTHENE