Classe :

CORRECTION
Une propriété de la bissectrice d’un angle
Cercle inscrit dans un triangle
Activité réalisée à l’aide d’un logiciel de géométrie
1ère PARTIE
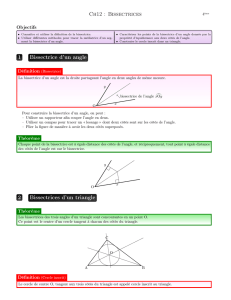
I Construction de la figure
1) Placer trois points O, A et B et
les nommer.
2) Tracer la demi-droite [OA) et
la demi-droite [OB).
3) Tracer la bissectrice de l’angle
AOB.
4) Placer un point M, distinct de
O, appartenant à la bissectrice
de l’angle AOB et le nommer.
II A la découverte de la propriété
1) Mesurer la distance de M à (OA) puis la distance de M à (OB). Pour cela vous effectuerez
les constructions nécessaires.
Quels résultats obtient-on ?
Les distances entre M et les côtés de l'angle sont les même
2) A l’aide de la souris, faire bouger le point M.
Que constate-t-on ?
Le point M restant sur la bissectrice , Les distances entre M et les côtés de
l'angle sont les même
3) A l’aide de la souris, faire bouger l’angle AOB en faisant bouger le point A.
Que constate-t-on ?
Quelque soit la mesure de l'angle AOB Les distances entre M et les côtés de
l'angle sont les même
III Propriété
Compléter la phrase suivante :
Si un point est situé à la même distance des côtés d'un angle alors il appartient à la bissectrice de
cet angle
Il existe aussi la réciproque :
Réciproquement, si un point appartient à la bissectrice d'un angle alors il est situé à la même
distance des côtés de cet angle.
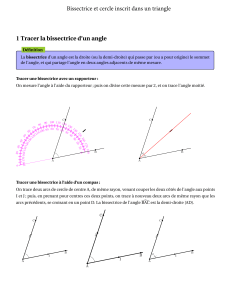
III Bissectrices d’un triangle
1) Tracer un triangle ABC.
2) Construire la bissectrice de l’angle ABC.
Construire la bissectrice de l’angle ACB.
Elles se coupent en I. Placer le point I.
3) Construire la bissectrice de l’angle BAC.
Que remarque-t-on ?
Les trois bissectrices des angles d'un triangle sont concourantes

Vérifier à l’aide du logiciel que le point I appartient à la bissectrice de l’angle BAC.
4) A l’aide de la souris, faire bouger le triangle en faisant bouger le point A.
La remarque est-elle encore valable ? oui
5) Compléter la phrase suivante :
Les trois bissectrices des angles d'un triangle sont concourantes
II Cercle inscrit dans un triangle
Pour que la figure soit plus claire, cacher les trois bissectrices à l’aide de la dernière icône.
Ne doivent rester visibles que le triangle et le point I, point d’intersection des bissectrices.
1) Construire la perpendiculaire à (AB) passant par I. Elle coupe (AB) en H.
Construire la perpendiculaire à (AC) passant par I. Elle coupe (AC) en K.
Construire la perpendiculaire à (BC) passant par I. Elle coupe (BC) en L.
2) Compléter le raisonnement suivant :
On sait que I appartient à la bissectrice de l’angle ABC.
Or si un point appartient à la bissectrice d’un angle
alors il est a égal distance des côtés de l'angle.
Donc IH = IL
De la même façon, I
appartient à la bissectrice de
l’angle ACB
Donc IK = IL
Donc IH = IL = IK
Donc H, K, L appartiennent à
un même cercle de centre I
3) Construire ce cercle.
4)
5) Que peut-on dire des côtés
du triangle par rapport au
cercle ?
Les côtés du triangles sont tangents au cercle car les rayons IK , IL, IH sont
respectivement Perpendiculaire aux côté [AC] , [BC] et [AB].
6) On dit que « Le point d’intersection des bissectrices d’un triangle est le centre du
cercle inscrit dans ce triangle ».