Bissectrice et cercle inscrit dans un triangle 1 Tracer

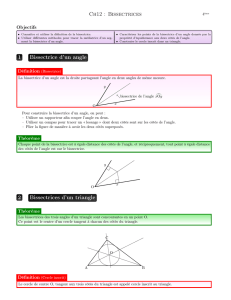
1 Tracer la bissectrice d’un angle
La bissectrice d’un angle est la droite (ou la demi-droite) qui passe par (ou a pour origine) le sommet
de l’angle, et qui partage l’angle en deux angles adjacents de même mesure.
Définition
Tracer une bissectrice avec un rapporteur :
On mesure l’angle à l’aide du rapporteur ; puis on divise cette mesure par 2, et on trace l’angle moitié.
0
180
10
170
20
160
30
150
40
140
50
130
60
120
70
110
80
100
90
90
100
80
110
70
120
60
130
50
140
40
150
30
160
20
170
180
0
A
B
C
A
B
C
Tracer une bissectrice à l’aide d’un compas :
On trace deux arcs de cercle de centre A, de même rayon, venant couper les deux côtés de l’angle aux points
I et J ; puis, en prenant pour centres ces deux points, on trace à nouveau deux arcs de même rayon que les
arcs précédents, se croisant en un point D. La bissectrice de l’angle  BAC est la demi-droite [AD).
A
B
C
I
J
A
B
C
I
J
A
B
C
I
J
Bissectrice et cercle inscrit dans un triangle

2 Tracer le cercle inscrit dans un triangle
Nous aurons besoin de cette propriété, admise :
•Si un point est situé sur la bissectrice d’un angle,
alors ce point est situé à égale distance des côtés de l’angle.
•Si un point est situé à égale distance des deux côtés d’un
angle,
alors ce point est situé sur la bissectrice de l’angle.
Propriété
I
K
H
Les bissectrices des angles d’un triangle se croisent en un même point ; on dit qu’elles sont concou-
rantes.
Le point commun à ces trois bissectrices est le centre du cercle inscrit dans ce triangle : chacun des
côtés du triangle est tangent à ce cercle.
Propriété
Illustration :
A B
C
Eléments de preuve :
•Le point I est situé sur la bissectrice de l’angle  BAC ; le point I est donc situé à égale distance des côtés
[AB] et [AC] ; on a donc IH=IK
•Le point I est situé sur la bissectrice de l’angle  ABC ; le point I est donc situé à égale distance des côtés
[AB] et [BC] ; on a donc IH=IL
•On en déduit que IH=IK=IL , et donc que les points H,K et L sont sur un cercle Cde centre I.
•De plus, la droite (BC) passe par le point I, et est perpendiculaire au rayon [IL] ; le côté [BC] est donc
tangent au cercle Cen L, et il en est de même pour les côtés [AB] et [AC]
On en conclut que I est le centre du cercle inscrit dans le triangle ABC.