2nde Thème : L`Univers Séquence : Le système solaire

Classe de 2nde – Séquence 1 : Le système solaire - page 1 / 6
(TP Professeur)
2nde
Thème : L’Univers
Séquence : Le système solaire
Problématique de la séance 1 :
Relativité du mouvement dans l’Univers
Pré requis :
Objectifs de la séance :
 Notion de référentiel
 Relativité des trajectoires
Connaissances :
 Comprendre que la nature du mouvement observé dépend du référentiel choisi
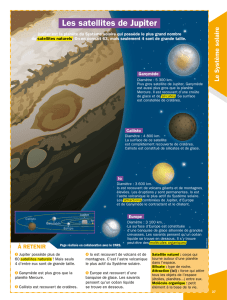
Les satellites de Jupiter. Mouvement rétrograde de mars.
Matériel élève
- Maquette de Jupiter et de ces satellites
- Ordinateur + Logiciel Stellarium
- Papier calque (carré de 10 cm sur 10 cm)
Matériel élève
- Ordinateur + Logiciel Stellarium + vidéoprojecteur
I Les satellites de Jupiter.
La lunette astronomique, inventée au début du XVIIe siècle, a permis à Galilée d’observer des
objets non visibles à l’œil nu.
Dans son ouvrage le Sidereus Nuncius (en français : Le Messager Céleste) publié en 1610, il
expose, sous la forme d’une narration accompagnée de dessins, qu’une lunette lui a permis
d’observer jour après jour la planète Jupiter et son voisinage. Le récit commence la nuit du 7
janvier 1610. Il explore le ciel aux abords de la planète.
« Je reconnus que trois petites étoiles, assurément menues mais très brillantes, étaient près de
Jupiter. Telle était leur disposition par rapport à rapport à Jupiter : deux étoiles se trouvent à
l’est (ORIENT) et une à l’Ouest (OCCIDENT)…… »
Il relève les positions de ce jour,
puis celles entre autres du 13 janvier 1610 et du 15janvier 1610
Jupiter est représenté par un cercle et ses satellites par des étoiles.
L’observation est faite depuis la ville de Padoue en Italie à 19H.
A. Simulation de l’observation de Galilée.
1. Observation au simulateur (gérée par le professeur).
- Réglage du lieu d’observation (Fenêtre de positionnement) : Padova, Italie.
- Réglage de la date et de l’heure (Fenêtre date/heure) : 1610/1/13 à 19.0.0
- Bloquer le défilement du temps (en bas à droite)
- Rechercher un objet (Fenêtre de recherche) : Jupiter
- Centrage de l’observation sur l’objet sélectionné : barre espace (ou clique sur l’icône).
- Zoom avec roulette de la souris

Classe de 2nde – Séquence 1 : Le système solaire - page 2 / 6
(TP Professeur)
- Si les satellites ne se présentent pas comme sur le dessin de Galilée, inverser la monture
équatoriale/azimutale (CTRL M)
2. Reproduire les schémas correspondants aux observations de Galilée du 13 et du 15 janvier
1610. Indiquer les noms des satellites de Jupiter.
Europe – Jupiter – Ganymède – Io – Callisto
- Pour passer au 15 janvier, aller simplement dans le fenêtre date et heure (toujours garder 19.0.0)
Jupiter – Io –Europe –Ganymède –Callisto
3. Pourquoi Galilée n’a-t-il représenté que trois satellites sur son schéma du 7 janvier 1610 ?
Plusieurs réponses sont possibles. Pour la suite, ne retenir que celle qui sera mise en évidence
avec le simulateur.
Callisto - Io et Europe (Europe juste devant Io et qui cache Io donc) – Jupiter – Ganymède.
B. Interprétation à l’aide d’une maquette.
Vous disposez d’une maquette sur laquelle les satellites (représentés par un point de couleur sur le
transparent) tournent autour de Jupiter (cercle noir au centre).
Depuis le centre de Jupiter, sur la feuille cartonnée, ont été tracés des rayons tous les dix degrés.
L’utilisateur de la maquette devra, pour faire ses observations, se placer dans le prolongement du
rayon portant l’indication : vers la Terre.
1. Utiliser la maquette pour retrouver l’observation du 7 janvier 1610 à 19H.
2. En utilisant les données suivantes, déterminer de combien de degrés se déplace chaque
satellite sur son orbite en un jour terrestre. Calculer la vitesse moyenne de chaque satellite.
Satellite de
Jupiter
Période de révolution
(en jours terrestres)
Rayon de l’orbite (105km)
Io
1,77
4,2
Europe
3,55
6,7
Ganymède
7,15
10,7
Callisto
16,69
18,8
Pour Io : nombre de degrés en un jour terrestre :
 203
1,77
360
,
vitesse moyenne :
14
5km.h6,2.10
1,7724 4,2.10π2 Δt
R2π
Δt
d
v
Pour Europe : nombre de degrés en un jour terrestre :
 101
3,55
360
,
vitesse moyenne :
14
5km.h4,9.10
3,5524 6,7.10π2 Δt
R2π
Δt
d
v
Pour Ganymède : nombre de degrés en un jour terrestre :
 50,3
7,15
360
,
vitesse moyenne :
14
5km.h3,92.10
7,1524 10,7.10π2 Δt
R2π
Δt
d
v
Pour Callisto : nombre de degrés en un jour terrestre :
 21,6
16,69
360
,
vitesse moyenne :
14
5km.h2,95.10
16,6924 18,8.10π2 Δt
R2π
Δt
d
v

Classe de 2nde – Séquence 1 : Le système solaire - page 3 / 6
(TP Professeur)
3. Positionner les satellites sur la maquette le 8 janvier à 19H. Faire le schéma
(schéma1) qu’a ou qu’aurait pu faire Galilée ce jour là. Vérifier au simulateur.
Callisto –Jupiter – Io –Europe –Ganymède
4. Galilée a réalisé ses observations depuis la Terre. Représenter (schéma 2) ce qu’aurait vu un
observateur situé sur Jupiter et regardant en direction de Io le 8 janvier à 19H. Comparer avec
le schéma 1.
5. Dans les deux schémas, on n’a pas choisi le même référentiel. Donner une définition de ce
terme. Quelle est l’obligation à respecter lorsqu’on veut décrire un mouvement ?
Un référentiel est un objet par rapport auquel on repère les positions successives du point dont on étudie le
mouvement. La trajectoire et la vitesse d'un point d'un objet dépendent du choix du référentiel.
Avant chaque étude de mouvement, il faut définir le référentiel d’étude.
6. A l’époque de Galilée, les savants affirmaient que tous les corps de l’Univers tournaient
autour de la Terre. En quoi la description de Galilée remet-elle en cause cette conception
géocentrique de L’Univers ?
Les satellites tournent autour du Jupiter, ben ils ne tournent pas autour de la Terre... Alors Galilée il a
raison et les autres ils ont tort!!! C'est simple, non!
II Mouvement de Mars.
Tout comme la Terre et les autres planètes du système solaire, la planète Mars tourne autour du
centre du Soleil. Depuis la surface de la Terre, un observateur constate cependant que le centre de la
planète Mars possède une trajectoire complexe. Quelle est cette trajectoire ? A montrer au simulateur
là ou à la fin.
Avec le logiciel :
- Réglage du lieu d’observation (Fenêtre de positionnement) : Paris.
- Réglage de la date et de l’heure (Fenêtre date/heure) : 2009/11/01 (1er novembre 2009) à 2.0.0
- Bloquer le défilement du temps (en bas à droite)
- Rechercher un objet (Fenêtre de recherche) : Mars
- Faire apparaître lignes et noms des constellations (en bas à gauche)
- Centrage de l’observation sur l’objet sélectionné : une des étoiles de la constellation du Cancer
- barre espace (ou clique sur l’icône).
- Dezoomer en faisant apparaître la Terre avec roulette de la souris
- Faire défiler le temps jour après jour (jusqu’à avril 2010)
Le document suivant représente vingt positions simultanées du centre de la Terre (T1, T2,…..) et du
centre de Mars (M1, M2,….) autour du Soleil.
1. Dans quel référentiel sont décrites les trajectoires de la Terre et de Mars sur ce document ?
Dans le référentiel héliocentrique.
Le référentiel héliocentrique a pour point fixe le centre du Soleil dont les axes pointent vers des étoiles
lointaines et dont les trois axes pointent vers des étoiles lointaines qui apparaissent fixe mais dont
l'origine est prise au centre du Soleil. Les expériences prouvent que l'on peut le considérer comme
galiléen avec une très bonne précision.
2. Tracer sur une feuille de papier calque deux droites perpendiculaires passant par le centre de
la feuille et noter T leur intersection.
Superposer le point T avec T1, les droites étant parallèles à celles déjà représentées sur le
document. Marquer la position M1 sur le calque.
Déplacer le calque en maintenant parallèle les droites du calque et celles du document pour
faire coïncider T avec T2 et marquer M2 sur le calque.
Etc… pour toutes les positions.
3. Quel référentiel est matérialisé par la feuille de papier calque ? Tracer la trajectoire du centre
de Mars sur la feuille de papier calque.
Le référentiel géocentrique.

Classe de 2nde – Séquence 1 : Le système solaire - page 4 / 6
(TP Professeur)
Le référentiel géocentrique est un référentiel dont l'origine est le centre de la Terre et dont les trois
axes pointent vers des étoiles lointaines qui apparaissent fixes.
Le référentiel géocentrique se distingue du référentiel terrestre, dont l'origine est prise au centre de la
Terre, mais dont les axes sont attachés au globe terrestre. Il est également différent du référentiel de
Kepler, dont les axes pointent vers des étoiles lointaines mais dont l'origine est prise au centre du
Soleil. Ainsi, le référentiel terrestre est en rotation dans le référentiel géocentrique, lui-même en
translation circulaire dans le référentiel de Kepler.
4. Les astronomes qualifient le mouvement de Mars de « mouvement rétrograde ». Proposer
une explication.
http://www.astronomes.com/c0_histoire/p011_syssol.html
(animation sur le mouvement de mars)
C'est le même phénomène qui explique le mouvement rétrograde de Mars par exemple. La plupart du
temps, cette planète se déplace vers l'est dans le ciel du fait de son mouvement de révolution. Cependant,
lorsque la Terre passe entre elle et le Soleil. Le déplacement de notre planète, plus rapide, crée un effet de
projection qui nous donne l'impression que la planète rouge se déplace dans l'autre sens, vers l'ouest. Ceci
continue jusqu'à ce que la Terre s'éloigne et que Mars reprenne son cheminement apparent normal. Comme
nous le verrons plus tard, le mouvement rétrograde des planètes a été le plus grand casse-tête des premiers
astronomes.
5. Comment se fait-il que le centre de Mars puisse avoir deux trajectoires différentes ?
Car la trajectoire dépend du référentiel d’étude choisi.

Classe de 2nde – Séquence 1 : Le système solaire - page 5 / 6
(TP Professeur)