lien document

Page 1 sur 3
DEVOIR SURVEILLE, classe de 1°S
(20 points ; 1h30min)
N.B.
- Deux points seront réservés à la qualité de la présentation et de la rédaction.
- Dans la mesure du possible toute réponse devra être justifiée.
Exercice 1 (5 points)
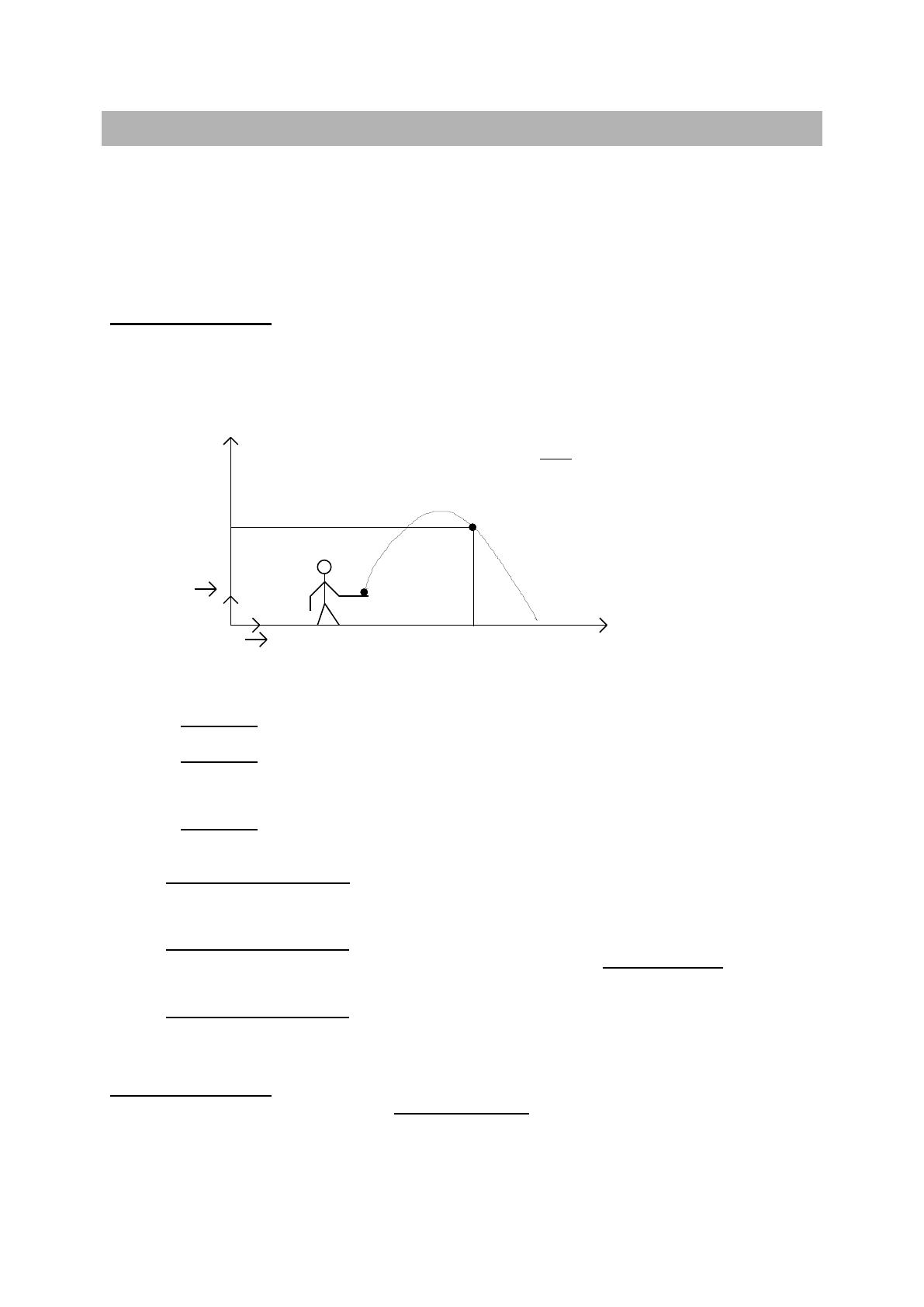
On a filmé le mouvement d’une balle de tennis en chute libre lancée avec vitesse initiale. Un logiciel de pointage
( « Aviméca ») permet d’obtenir les coordonnées (xi, yi) du centre d’inertie G de la balle dans le repère
orthonormal ( O,
i
,
j
) aux différentes dates ti du mouvement.
O
j
ix
y
: trajectoire de la balle
i
i
x
y
A l’aide de logiciels adaptés on obtient les documents 1,2 et 3 figurant en annexe :
- le document 1 représente les positions successives G0, G1, G2, …, G22 du point G aux différente dates
t0, t1,t2,…, t22 du mouvement.
- le document 2 est une feuille de tableur (« Excel ») elle donne aux différentes dates ti du mouvement
les valeurs des coordonnées (xi,yi) du point G ; les coordonnées (Vxi, Vyi) et la valeur Vi du vecteur
vitesse
i
V
du point G ;
- le document 3 représente l’évolution des valeurs de Vxi, Vyi et de Vi en fonction de la date ti du
mouvement.
1. A l’aide du seul document 1 évaluer la valeur V10 du vecteur vitesse du centre d’inertie de la balle en
G10 (date t10 = 0,40 s). La valeur trouvée est-elle conforme à celle indiquée dans le document 2 ?
Représenter en G10 le vecteur vitesse
10
V
(préciser l’échelle de représentation).
2. On considère le document 2. La ligne correspondant à la position G5 du centre d’inertie de la balle est
incomplète. Compléter cette ligne en indiquant les calculs à effectuer. Sur le document 1 représenter
en G5 le vecteur vitesse
5
V
. Le vecteur vitesse est-il constant au cours du mouvement (justifier) ?
3. On considère le document 3 que peut-on dire du mouvement de la balle selon l’axe des abscisses
(Ox) ? On peut distinguer deux phases lors du mouvement du centre d’inertie de la balle. Quelles sont
ces deux phases (justifier) ?
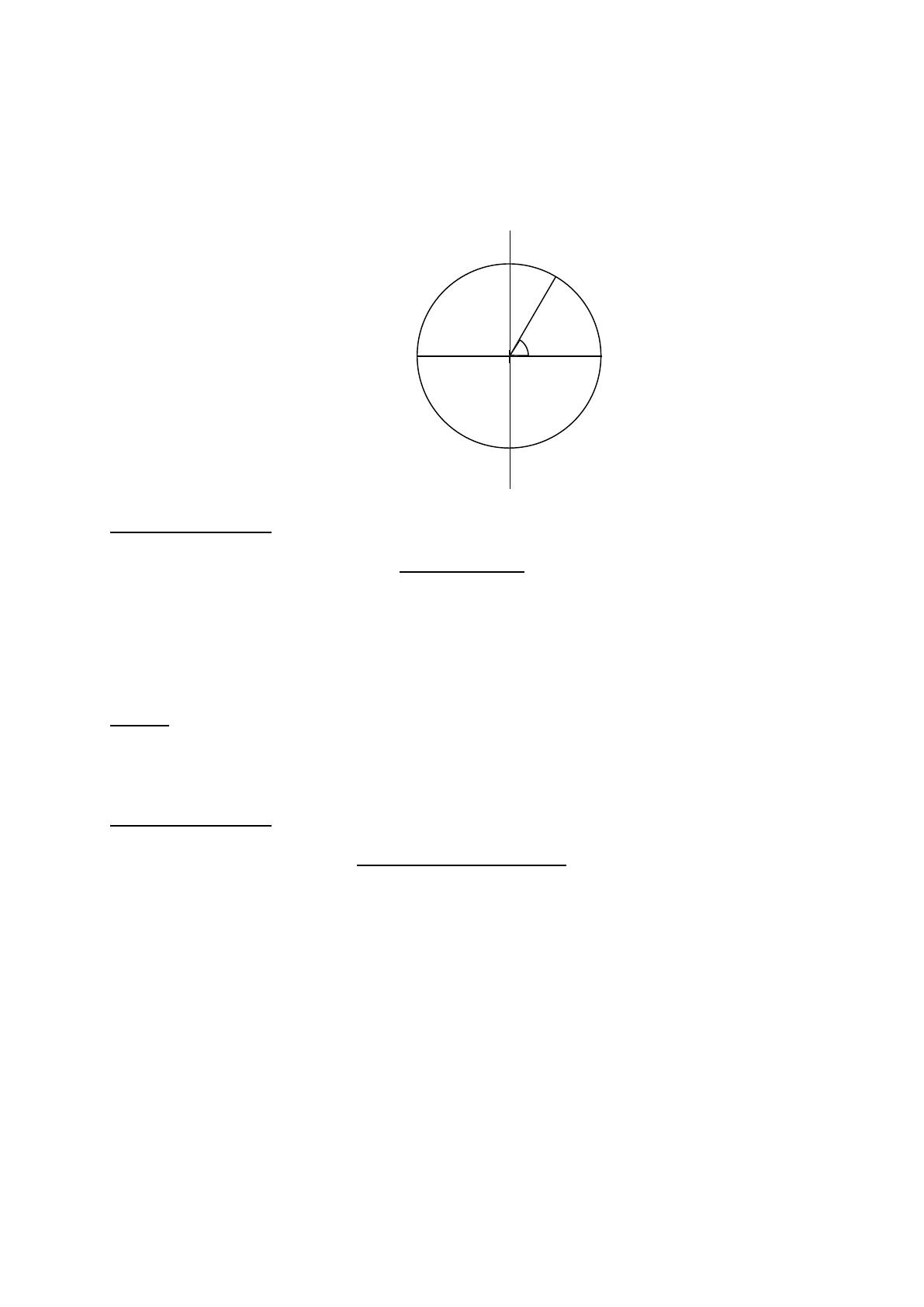
Exercice 2 (3 points) Rotation de la Terre
1. La période de rotation de la Terre ( rayon RT = 6380 km) autour de l’axe de ses pôles, dans le référentiel
géocentrique, est de 86 164 s ( durée pour effectuer un tour autour de son axe).

Page 2 sur 3
Calculer la valeur de la vitesse (en m.s-1) d’un point :
- A1 situé sur l’équateur ;
- A2 situé à une latitude  de 60° nord (ou sud).
Equateur
N
S Axe des pôles
A
A
=60°
1
2
Exercice 3 (5 points)
Solide à l’équilibre
Un motif décoratif illuminé, de masse m = 40 kg, est suspendu entre deux immeubles par deux câbles, faisant
l’un et l’autre un angle  = 40 ° avec la verticale.
Déterminer graphiquement les valeurs des forces exercées par chacun des câbles sur le motif décoratif.
Une justification rigoureuse de votre construction est attendue.
Donnée :
- Valeur de l’intensité de la pesanteur : g = 10 N.kg-1
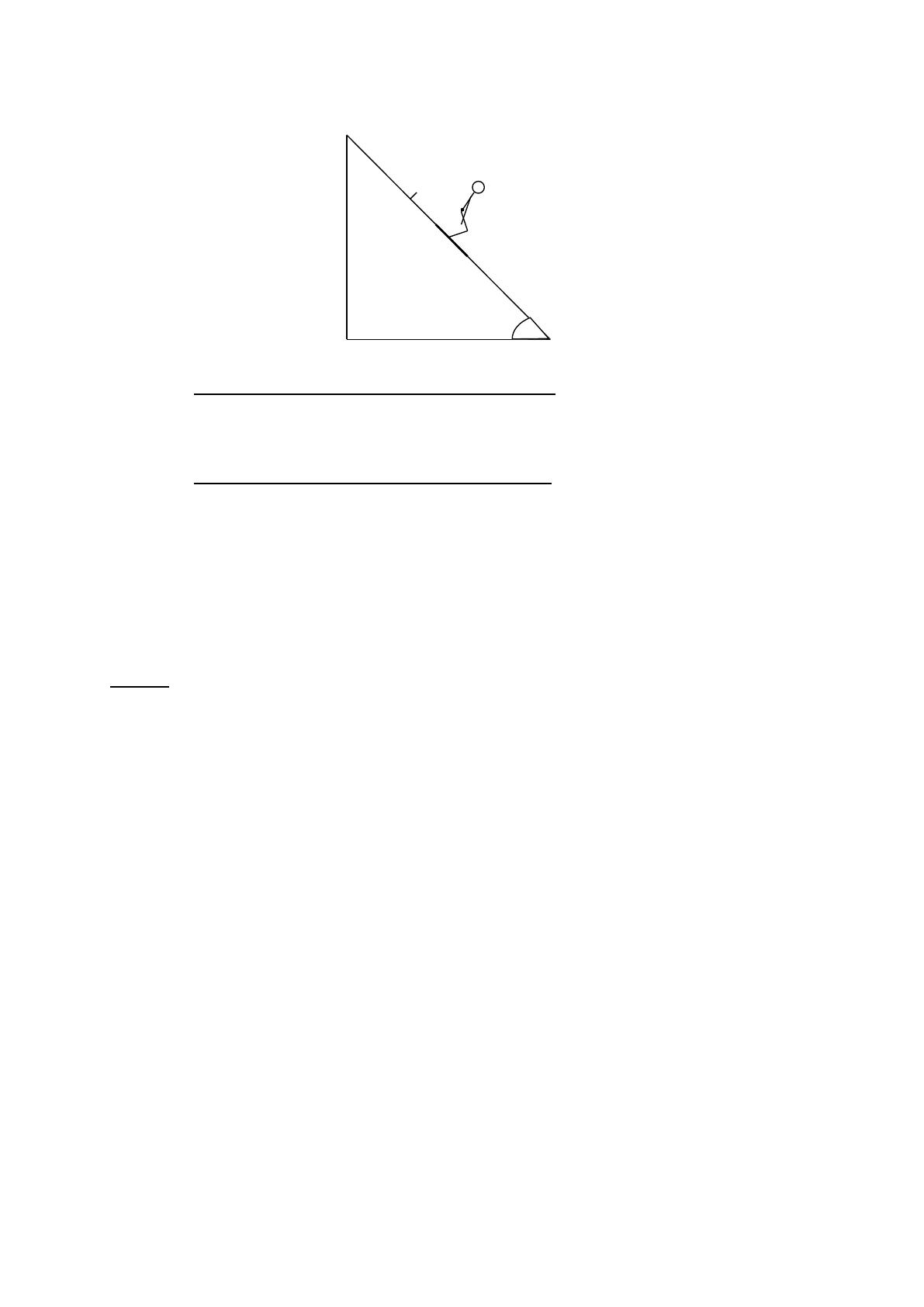
Exercice 4 (5 points)
Applications des lois de Newton
Les parties I et II sont indépendantes.
Un sauteur à ski de masse m = 80 kg , dévale la piste d’élan, plane, faisant avec l’horizontale un angle de 45°.
Le skieur est d’abord animé d’un mouvement de translation rectiligne accéléré sur la portion AB de la piste,
puis sa vitesse se stabilise (est constante) sur la portion BC de la piste.

Page 3 sur 3
A
C
B
45°
G
I) MOUVEMENT DU SKIEUR SUR LA PORTION AB
En utilisant la deuxième loi de Newton déterminer la direction et le sens de la résultante des forces appliquées au
skieur.
II) MOUVEMENT DU SKIEUR SUR LA PORTION BC
1. Quelle est la nature du mouvement du skieur lorsque sa vitesse se stabilise.
2. Effectuer un bilan des forces appliquées au skieur dans cette phase du mouvement.
3. Enoncer la première loi de Newton (ou principe d’inertie), puis établir une relation entre les forces
appliquées au skieur.
4. Schématiser le skieur et représenter les forces qui lui sont appliquées, à l’échelle 1cm représente 200 N.
5. Déterminer graphiquement, puis par le calcul la valeur f de la force de frottement exercée par la piste
sur le skieur.
6. Déterminer les caractéristiques de la force
F
exercée par le skieur sur la piste.
Donnée :
- Valeur de l’intensité de la pesanteur : g = 10 N.kg-1