Evolution concepts géométrie

Projet de développement 2006 : Le passage primaire/secondaire en mathématique
Équipe de travail
S. Blais, I. Gendron, 22 mars 2006
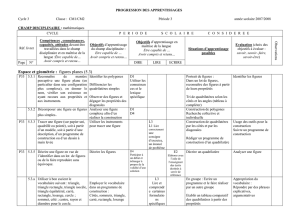
Évolution des concepts liés à la géométrie dans les programmes de formation du primaire et du secondaire
Préscolaire
1er cycle
2e cycle
3e cycle
1er cycle
Sens de la
compétence
 L’élève construit sa
compréhension du
monde à mesure qu’il
découvre dans son
milieu les arts, l’univers
social, la
mathématique, la
science et la
technologie.
 L’élève dégage des
régularités
géométriques
facilement observables.
 L’élève décrit et classifie les
objets géométriques selon leurs
attributs. Il construit des
relations géométriques
complexes.
 L’élève poursuit l’étude d’objets géométriques selon
leurs attributs et la construction de relations
géométriques.
Sens de la
compétence
 L’élève passe de l’observation au raisonnement. Il
énonce et mobilise des propriétés, des définitions et
des relations pour analyser et résoudre une
situation-problème. Il construit des figures au
besoin, à l’aide d’instruments ou de logiciels de
géométrie dynamique, et il manipule des
expressions numériques ou algébriques, en
particulier pour le calcul de longueurs et d’aires.
L’élève interprète et écrit les résultats numériques
obtenus en utilisant les unités de mesure
appropriées à la situation.
 L’élève déploie un raisonnement lorsqu’il apprend à
reconnaître les caractéristiques des figures usuelles,
met en évidence leurs propriétés et effectue des
opérations sur les figures planes à l’aide de
transformations géométriques. Il compare et calcule
des angles, des longueurs et des aires, et il forme
des patrons (développements) de solides qu’il
représente par un dessin. Il se familiarise avec les
définitions et les propriétés des figures qu’il utilise
pour résoudre des problèmes à l’aide de déductions
simples. Il détermine des mesures manquantes
dans différents contextes.
Les attentes de
fin de cycle
 Il utilise quelques
éléments de base des
différents domaines
d’apprentissage que
sont les arts, l’univers
social, la
mathématique, la
science et la
technologie.
 L’élève construit des
figures planes et des
solides.
 L’élève peut décrire des
figures planes et des solides.
 L’élève peut décrire et classifier des figures planes et
reconnaître le développement de polyèdres convexes.
Les attentes
de fin de cycle
 L’élève construit des figures, identifie des propriétés
ainsi que des relations entre les propriétés des
figures et utilise des définitions. Pour le calcul de
longueurs et d’aires, il émet un raisonnement sur les
formules en manipulant des expressions
numériques ou algébriques et interprète les résultats
obtenus.
 L’élève procède par des déductions simples à partir
de définitions et de propriétés, par exemple pour
déterminer la valeur de mesures manquantes.

Projet de développement 2006 : Le passage primaire/secondaire en mathématique
Équipe de travail
S. Blais, I. Gendron, 22 mars 2006
Préscolaire
1er cycle
2e cycle
3e cycle
1er cycle
Les échelles
des niveaux de
compétence
Inexistant
Échelon 1 : L’élève
compare, ordonne et
classifie des objets selon
une dimension. Il est
capable de se repérer dans
l’espace, de nommer et de
comparer des figures planes
et des solides à des objets
de son environnement.
Échelon2 : sans précision
Échelon 3 : L’élève
compare et construit des
figures planes.
Échelon 4 : L’élève décrit des
prismes et des pyramides.
Échelon 5 : L’élève effectue du
repérage dans un plan. Il construit
des frises et des dallages à l’aide de
réflexions.
Échelon 6 : L’élève classifie des
quadrilatères. Il construit des frises
et des dallages à l’aide réflexions.
Échelon 7 : L’élève effectue du repérage dans le plan
cartésien. Il construit des frises et des dallages à l’aide de
translations.
Échelon 8 : L’élève classifie des triangles.
Échelon 9 : L’élève classifie des triangles. Il construit des
frises et des dallages à l’aide de translations. Il effectue du
repérage dans le plan cartésien.
Les échelles
des niveaux
de
compétence
À venir
Les savoirs
essentiels
 Les jeux d’association
(ex. : associer un objet
à une forme
géométrique), de
regroupement et de
classement (ex. :
classer des objets selon
la couleur, la texture, la
forme), de régularité
(ex. : créer des suites
d’objets de plus en plus
complexes).
 Les concepts d’espace
(ex. : haut, bas, près,
loin milieu, grand,
large).
Espace :
 Repérage d’objets et de
soi dans l’espace,
relations spatiales
(devant, sur, à gauche,
etc).
 Repérage sur un axe,
dans un plan,
Solides :
 Comparaison et
construction : prisme,
pyramide, boule,
cylindre, cône.
 Comparaison des
objets de
l’environnement aux
solides.
 Attributs (nombre de
faces, base) : prisme,
pyramide
Figures planes :
 Comparaison et
construction de figures
composées de lignes
Espace :
 Repérage sur un axe, dans un
plan et dans le plan cartésien.
 Description de polygones
convexes et non convexes
Solides :
 Description de prismes et de
pyramides à l’aide de faces, de
sommets et d’arêtes
 Développement et classification
de prismes et de pyramides
Figures planes :
 Description de polygones
convexes et non convexes.
 Description des quadrilatères
dont le trapèze et le
parallélogramme : segments
parallèles, segments
Espace :
 Repérage sur un axe et dans le plan cartésien.
Solides :
 Reconnaissance du développement de polyèdres
convexes
 Expérimentation de la relation d’Euler (relation entre les
faces, les sommets et les arêtes d’un polyèdre
convexe).
Figures planes :
 Description de triangles : triangle rectangle, triangle
isocèle, triangle scalène, triangle équilatéral
 Classification des triangles
Contenu de
formation
(concepts et
processus)
 Figures planes
-Triangles, quadrilatères et polygones réguliers convexes
-Segments et droites remarquables : bissectrice,
médiatrice, médiane, hauteur
- Base, hauteur
 Cercle, disque et secteur
- Rayon, diamètre, corde, arc
- Angle au centre
--Angles
 Complémentaires, supplémentaires
 Créés par deux droites sécantes : opposés par le
sommet, adjacents
 Créés par une droite sécante à deux autres droites :
alternes-internes, alternes externes,
correspondants
- Constructions géométriques
- Transformations géométriques
 Translation, rotation, réflexion
 Homothétie de rapport positif

Projet de développement 2006 : Le passage primaire/secondaire en mathématique
Équipe de travail
S. Blais, I. Gendron, 22 mars 2006
Préscolaire
1er cycle
2e cycle
3e cycle
1er cycle
courbes fermées ou de
lignes brisées fermées
 Identification du carré,
du rectangle, du
triangle, du cercle et du
losange
 Description du carré, du
rectangle, du triangle et
du losange
Frises et dallages :
 Figures isométriques
(mêmes mesures)
perpendiculaires, angle droit,
angle aigu, angle obtus
 Classification des quadrilatères
 Construction de lignes parallèles
et de lignes perpendiculaires
Frises et dallages :
 Observation et production de
régularités à l’aide de figures
géométriques
 Observation et production
(grilles, papier calque) de frises
par réflexions : réflexion et axe
de réflexion
 Observation et production de
dallages à l’aide de la réflexion
 Mesure d’angles en degrés à l’aide d’un rapporteur
d’angles
 Étude du cercle : rayon, diamètre, circonférence, angle
au centre
Frises et dallages :
 Observation et production (grilles, papier calque) de
frises par translation : translation, flèche de translation
(longueur, direction, sens)
 Observation et production de dallages à l’aide de la
translation.
Les repères
culturels
 L’exploitation de
logiciels
 Contexte
interdisciplinaire ou
social (ex. :
architecture, cartes
géographiques, arts,
décoration)
 Contexte interdisciplinaire ou
social (ex. : architecture, cartes
géographiques, arts,
décoration)
 Symboles (origine, évolution,
besoin, mathématicien et
mathématicienne) : ┴, //,
 Contexte interdisciplinaire ou social (ex. : architecture,
cartes géographiques, arts, décoration)
 Symboles (origine, évolution, besoin, mathématicien et
mathématicienne) : ┴, //,
Les repères
culturels
Éléments de
méthode
Inexistant
Inexistant
Inexistant
Inexistant
Éléments de
méthode

Projet de développement 2006 : Le passage primaire/secondaire en mathématique
Équipe de travail
S. Blais, I. Gendron, 22 mars 2006
Préscolaire
1er cycle
2e cycle
3e cycle
1er cycle
Symboles
Inexistant
Aucune information
┴, //,
┴, //,
Symbole
Inexistant
Vocabulaire
Inexistant
Base d’un solide, boule,
carré, cercle, cône, côté,
cube, cylindre, droite
numérique, face, figure
plane, losange, prisme,
pyramide, rectangle, solide,
suite, triangle
Angle obtus, angle aigu, angle droit,
arête, axe de réflexion, corps rond,
dallage, développement d’un solide,
…est parallèle à …, …est
perpendiculaire à …, figure
symétrique, frise, parallélogramme,
plan, plan cartésien, polygone,
polygone convexe, polygone non
convexe, quadrilatère, réflexion,
segment, sommet, surface, surface
courbe, surface plane, système de
repérage, trapèze,
Angle au centre, circonférence, degré (angle), diamètre,
disque, flèche de translation, polyèdre, polyèdre convexe,
rapporteur d’angles, rayon, relation d’Euler, translation,
triangle équilatéral, triangle isocèle, triangle scalène,
triangle rectangle,
Vocabulaire
Inexistant
Énoncés de
Géométrie
Euclidienne
Inexistant
Inexistant
Inexistant
Inexistant
Énoncés de
Géométrie
Euclidienne
Voir énoncé p.261
Utilisation des
technologies
 L’exploitation de
logiciels comme
repères cuclturels.
 Utiliser l’ordinateur
(logiciel de dessin) pour
l’application de
différentes stratégies de
résolution de
problèmes.
 Utiliser l’ordinateur
(logiciel de dessin) pour
diffuser l’information
relative à la solution.
 Produire un dessin
(solides, figures planes,
frises et dallages) à
l’aide d’un logiciel à
dessin.
 Utiliser l’ordinateur (logiciel de
dessin) pour l’application de
différentes stratégies de
résolution de problèmes.
 Utiliser l’ordinateur (logiciel de
dessin) pour diffuser l’information
relative à la solution.
 Produire un dessin (solides,
figures planes, frises et dallages)
à l’aide d’un logiciel à dessin.
 Utiliser Internet pour la
recherche de récits historiques
en rapport avec les concepts
étudiés.
 Consulter des sites Internet à
caractère mathématique, des
lexiques et des bases de
données.
 Utiliser l’ordinateur (logiciel de dessin) pour l’application
de différentes stratégies de résolution de problèmes.
 Utiliser l’ordinateur (logiciel de dessin) pour diffuser
l’information relative à la solution.
 Produire un dessin (solides, figures planes, frises et
dallages) à l’aide d’un logiciel à dessin.
 Utiliser Internet pour la recherche de récits historiques
en rapport avec les concepts étudiés.
 Consulter des sites Internet à caractère mathématique,
des lexiques et des bases de données.
Utilisation des
technologies
Inexistant