Calcul des rayons d`orbite r

Chimie
Quantification des niveaux d’énergie électronique
Introduction
Les limites du modèle planétaire.
D’après la mécanique classique :
(1) l’électron devrait émettre un rayonnement (électromagnétique)
(2) l’électron devrait être précipité sur le noyau
(3) l’électron devrait émettre une radiation continue au fur et à mesure qu’il est « accéléré » vers
le noyau
Or
(1) l’atome n’émet pas de rayonnement spontanément
(2) Les atomes sont stables
(3) Les spectres d’émission des atomes sont discontinus
1910-1920 : Construction d’un nouveau modèle (Atome de Bohr) à partir des interactions
matière/lumière (ondes électromagnétiques).
{ Limiter l’énergie à des valeurs discrètes est ce que l’on appelle la quantification de l’énergie. }
1- Lumière et ondes électromagnétiques : caractère ondulatoire
Rappel sur les ondes :
Ex : onde dans l’eau = vague
Les ondes électromagnétiques n’ont pas besoin de matière
Description mathématique :
Onde sinusoïdale : φ = φ
0 . sin (ω t)
 temps
Φ = φ
0 . sin (k x)
 espace
Propagation à vitesse, C = 2,998 x108 m.s-1  célérité de la lumière (dans le vide)
(2ème schéma)
Les ondes électromagnétiques sont caractérisées par :

- une période T (en s) - une longueur d’onde λ (en m)
- une fréquence ט (en Hertz) - un nombre d’onde σ (en m-1)
ט = 1/T σ = 1/λ
ט = c/λ
2- Le spectre électromagnétique
 spectre
Infra Rouge > visible > Ultra Violet
3- Lumière et ondes électromagnétiques : caractère corpusculaire
Postulat de Planck
(Max Planck, physicien allemand, 1858-1947, prix Nobel 1918)
● Echanges matière-rayonnement : Seules certaines valeurs d’énergie possibles.
La plus petite énergie échangeable est le quantum :
E = h ט
Avec ט, la fréquence de la radiation émise ou absorbée (en Hz) et h, la constante universelle (
h=6,626 x10-34 J.s-1)
● Echanges d’énergétique avec les atomes :
- Absorption d’un rayonnement de fréquence ט
 Energie augmentée de la quantité hט
- Emission d’un rayonnement de fréquence ט
 Energie diminuée de la quantité hט
{ Planck explique notamment la distribution d’énergie observée expérimentalement en
supposant que les énergies permises d’un oscillateur électromagnétique de fréquence ט sont des
multiples entiers de hט : E = nhט n=0, 1, 2,…
h = constante de Planck }
4- L’effet photoélectrique : mise en évidence des photons
Effet photoélectrique : certains métaux soumis à des radiations UV émettent des
électrons à partir d’une certaine fréquence et indépendamment de l’intensité de la radiation.
ΔUR : potentiel retardateur
Conclusion expérimentale :
Schéma 1 : Plaque métallique sous lumière UV.
 Emission d’électrons
Schéma 2 : Electrons accélérés ou ralentis suivant le potentiel ΔU entre les plaques.
 Observation d’un courant d’intensité i

Les deux schémas :
Fréquence minimale ט0 (ou seuil d’excitation) est fonction du métal.
E0 = h x ט0 C’est l’énergie minimum d’extraction de l’électron
Si E > E0 , électrons éjectés avec énergie cinétique T
Interprétation :
Sur la plaque émettrice (A) Au niveau de la plaque réceptrice (B)
TA = E – E0 = h (ט – ט0 ) TB – TA = e . ΔU
Si i > 0 TB > 0 C’est à dire TA + e . ΔU > 0
Si i → 0 TB → 0 C’est à dire TA + e . ΔU = 0
Ceci s’observe pour ΔU = ΔUR
Le potentiel retardateur
TA = -e . ΔUR = h . (ט – ט
0 )
ΔUR = - h/e . (ט – ט0 )
|ΔU| = f (ט) est une droite
Coefficient directeur h/e
5- Double caractère corpusculaire et ondulatoire de la lumière
{ Le caractère corpusculaire du rayonnement électromagnétique : Le résultat expérimentale
démontrant qu’un rayonnement électromagnétique de fréquence ט ne peut posséder que les
énergies 0, hט, 2hט,… tend à prouver qu’il est constitué de 0,1,2,… particules ayant chacune une
énergie hט. Ainsi, chaque particule présente possède une énergie égal à hט ; pour deux
particules, elle est 2hט, etc. Ces particules du rayonnement électromagnétique sont appelées
des photons. Les raies des spectres des atomes et des molécules sont produites lorsqu’un atome
ou une molécule émet un photon d’énergie hט en perdant une quantité d’énergie ΔE = hט
nombre de photon : N → N = E/(hט)
On peut expliquer l’effet photoélectrique en supposant que le rayonnement incident est
composé de photons ayant une énergie proportionnelle à la fréquence du rayonnement.}
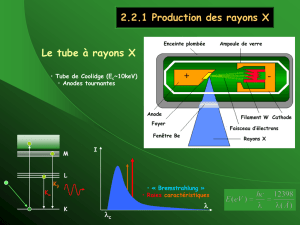
6- Spectre continus et discontinus Analyse spectrale
7- Les spectres atomiques

8- Le spectre de l’hydrogène
Johann Jakob Balmer (1825-1898), professeur de mathématiques suisse.
Manipulation des valeurs numériques :
→ formule pour prévoir toutes les longueurs d’ondes.
● Les longueurs d’onde des raies sont liées par la relation :
1/ λ = RH (1/n21 – 1/n22 ) Formule de Balmer
λ : longueur d’onde (en m)
RH = 1,1 x107 m-1 = Constante de Rydberg
n1 et n2 sont des chiffres entiers et n2 > n1
● L’ensemble de ces raies a été classé en « séries » :
Lyman (n1 = 1 ; UV)
Balmer (n1 = 2 ; visible)
Paschem (n1 = 3 ; IR)
Brackett (n1 = 4 ; IR)
● Chaque série présente l’allure suivante (ici pour Balmer) :
La raie de tête est la raie de plus grande longueur d’onde, pour une série donnée.
Elle correspond à :
n2 = n1 + 1 1/ λ tête = RH ( 1/n21 – 1/(n1+1)2)
La raie limite est la raie de plus petite longueur d’onde pour une série donnée.
Elle correspond à :
n2 → ∞ 1/ λ lim = RH ( 1/n21)
9- Le modèle de Bohr
Niels Bohr, physicien danois (1885-1962, prix Nobel 1922)
Construction d’un modèle de l’atome :
- à partir du modèle planétaire
- intégrant la quantification (à l’aide de chiffres entiers)

Interprétation des spectres discontinus observés.
Explication pour la formule de Bohr.
Modèle planétaire
Force centrifuge
F1 = m _ = mv2/r
Force électrostatique
F2 = - 1/(4π ε0) x e2/r2
v = vitesse de rotation
ε = charge e- et protons
a) Equilibre des forces : centrifuge/centripète :
mv2/r - 1/(4π ε0) x e2/r2 = 0
Calcul de l’énergie totale E :
L’énergie cinétique T est : T = ½ mv2
m = masse de l’électron
L’énergie potentielle V ou Ep représente le travail de la force électrostatique pour amener
l’électrons de l’infini jusqu’à la distance d’équilibre r soit :
V = - 1/(4π ε0) x e2/r2
L’énergie totale E = E cinétique + E potentielle
E = ½ mv2 - 1/(4π ε0) x e2/r2
Or mv2/r - 1/(4π ε0) x e2/r2 = 0
Equilibre des forces
E = ½ x 1/(4π ε0) x e2/r2 - 1/(4π ε0) x e2/r2 = - 1/(4π ε0) x e2/2r2
E = - 1/(4π ε0) x e2/2r2
Energie de l’électron sur un orbite de rayon r.
b) Quantification du moment angulaire
c) Conséquences :
• il existe des orbites stables de rayon rn