Exercice 1: étude expérimentale de dipôles

Corrigé Exercice 1 : ETUDE EXPERIMENTALE DE DIPOLES ELECTRIQUES
1. Dipôles « résistance et condensateur en série »
1.1.1. Car le phénomène observé n’est pas périodique
1.1.2. Les tensions observées sur l’oscilloscope ont
leur origine sur la borne « masse », sauf sur la voie B
si le bouton « –YB » est enfoncé. C’est le cas ici pour
la tension uR que l’on souhaite observer.
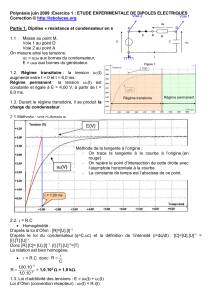
1.1.3. Régime transitoire : la tension uC(t)
augmente entre t = 0 et t = 6,0 ms.
Régime permanent : la tension uC(t) est
constante et égale à E = 4,00 V, à partir
de t = 6,0 ms.
1.1.4. Durant le régime transitoire, il se produit la
charge du condensateur à travers la résistance R.
1.2.1. Voir cours
1.2.2. Méthode : voir ci-contre R = /C = 1,00.10-3/1,0.10-6 = 1,0.103Ω
1.3.1. Loi d’additivité des tensions (ou loi des mailles): E - uR - uC = 0 donc E = uR + uC
1.3.2. Loi d’Ohm (convention récepteur) : uR = R.i
donc E = R.i + uC  i = (E-uC)/R
Pour t0 = 0 ms, uC = 0 V donc
i0 = E/R = 4,0.10–3 A = 4,0 mA.
Pour t1 = 1,0 ms, uC = 2,5 V donc :
i1 = (4-2,5)/ 1,0.103 = 1,5.10–3 A = 1,5 mA.
Allure du graphe i(t) : l’intensité décroît exponentiellement de 4,0 mA jusqu’à tendre vers 0 A.
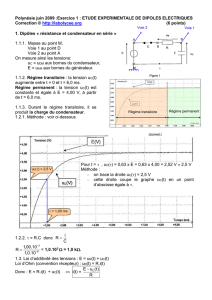
2. Dipôle « résistance et bobine en série »
2.1. Loi d’Ohm (convention récepteur) : uR’ = R’.i. La tension uR’ est proportionnelle à l’intensité i
qui circule dans le circuit après la fermeture de l’interrupteur K.
2.2. On observe le retard de l’établissement du courant i(t) dans le circuit.
La bobine est la cause de ce retard.
2.3. Loi d’additivité des tensions : E = uL + uR’
avec uL = r.i + L.
di
dt
et uR’ = R’.i
Donc E = L.
di
dt
+ (R’ + r).i
Pour t =  , uC() = 0,63 x E =
0,63 x 4,00 = 2,52 V  2,5 V
uC()
= 2,5
V
 = 1,00 ms
i(mA)
t(ms)
0
4,0
9
uL
Voie B inversée
Voie A
uR
Figure 1
E
P
uC
C
G
N
R
K
S
i
D

2.4. En régime permanent, i =Cte donc
di
dt
= 0.
L’équation différentielle devient : E = (r + R’).IP
2.5. r + R’ = 5,8 / 2,90.10-1 = 20Ω
donc r = 20-10 = 10Ω
3. Dipôle « bobine et condensateur en série »
3.1. Lorsque l’interrupteur est en position 1, il se produit la charge du condensateur…
nécessaire avant de pouvoir effectuer une décharge.
La constante de temps ( = R.C) est très faible car il n’y a pas de résistance dans le
circuit de charge et que la résistance des fils est quasi-nulle. Ainsi la charge du
condensateur est instantanée.
3.2. La décharge du condensateur dans la bobine met en évidence des oscillations
électriques libres et amorties.
3.T’0 = 2,0ms donc T’0 = 0,67ms. T’0 = 2.π.
CL.
3.3. Energie électrique accumulée dans le condensateur : Ee = ½.C.uC²
Energie magnétique accumulée dans la bobine : Em = ½.L.i²
3.4.1. Avant la fermeture du circuit de décharge, le condensateur est chargé et la tension à ses bornes
ne peut pas varier brutalement donc uC(0) = E’  0 V . Ainsi Ee(0 ) = ½.C.E²  0 J.
La courbe a est associée à Ee puisqu’elle ne passe pas par l’origine.
Avant la fermeture du circuit de décharge, i = 0 dans la bobine. Or celle-ci empêche l’intensité du
courant de varier brutalement donc i(0) = 0 A . Ainsi Em(0 ) = 0 J.
La courbe b est associée à Em puisqu’elle passe par l’origine.
3.4.2. Graphiquement : Ee(t1) = Em(t1) = 2,5 µJ
3.4.3. L’énergie totale du circuit à un instant t est : ET(t) = Ee(t) + Em(t)
Elle diminue au cours du temps.
Cette évolution est due à la dissipation d’énergie sous forme de chaleur, due à l’effet Joule,
dans la résistance r de la bobine.
3.4.4. On mesure sur une des deux courbes 3.T0 = 1,0ms soit T0 = 0.33ms
La période correspondant à la variation d’énergie emmagasinée par la bobine ou le condensateur
correspond à la moitié de la pseudo-période des oscillations
IP = 290 mA