Correction

Polynésie juin 2009 :Exercice 1 : ETUDE EXPERIMENTALE DE DIPOLES ELECTRIQUES
Correction © http://labolycee.org
Partie 1. Dipôles « résistance et condensateur en série »
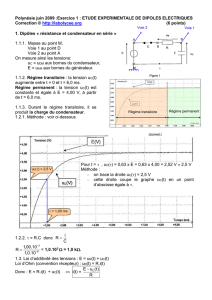
1.1 Masse au point M,
Voie 1 au point D
Voie 2 au point A
On mesure ainsi les tensions:
uC = uDM aux bornes du condensateur,
E = uAM aux bornes du générateur.
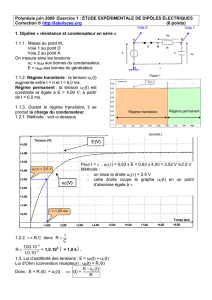
1.2. Régime transitoire : la tension uC(t)
augmente entre t = 0 et t = 6,0 ms.
Régime permanent : la tension uC(t) est
constante et égale à E = 4,00 V, à partir de t =
6,0 ms.
1.3. Durant le régime transitoire, il se produit la
charge du condensateur.
2.1 Méthode : voir ci-dessous
2.2.  = R.C
 Homogénéité :
D’après la loi d’Ohm : [R]=[U].[I]-1
D’après le loi du condensateur (q=C.uc) et la définition de l’intensité (i=dq/dt) : [C]=[Q].[U]-1 =
[I].[T].[U]-1
Donc [R].[C]= [U].[I]-1. [I].[T].[U]-1=[T]
La relation est bien homogène.
  = R.C donc
RC
3
6
1,00.10
R1,0.10
= 1,0.103  = 1,0 k.
1.3. Loi d’additivité des tensions : E = uR(t) + uC(t)
Loi d’Ohm (convention récepteur) : uR(t) = R.i(t)
Régime transitoire
Régime permanent
Voie 2
Voie 1
Méthode de la tangente à l’origine :
- On trace la tangente à la courbe à l’origine.(en
rouge)
- On repère le point d’intersection de cette droite avec
l’asymptote horizontale à la courbe.
- La constante de temps est l’abscisse de ce point.
 = 1,00 ms

Donc : E = R.i(t) + uC(t)  i(t) =
C
E u (t)
R
Pour t1 = 0 ms, uC(t1) = 0 V donc : i(t1) =
3
E 4,0
R 1,0.10
= 4,0.10–3 A = 4,0 mA.
Pour t2 = 9 ms, uC(t2) = E = 4,0 V donc : i(t2) =
C2 3
E u (t ) 4,0 4,0
R 1,0.10
= 0 A.
Allure du graphe i(t) : l’intensité
décroît exponentiellement de 4,0 mA
jusqu’à tendre vers 0 A.
Partie 2 : Dipôle « résistance et bobine en série »
1. Loi d’Ohm (convention récepteur) : uR’(t) = R’.i(t). La tension uR’(t) est proportionnelle à l’intensité
i(t) qui circule dans le circuit après la fermeture de l’interrupteur K. Connaissant les valeurs de uR’(t) et
la valeur de R’ (R’ = 10 ) on peut faire calculer à l’ordinateur les valeurs de l’intensité : i(t) =
R' R'
u (t) u (t)
R 10
.
2. On observe le retard de l’établissement du courant i(t) dans le circuit. La bobine est la cause
de ce retard.
3. Loi d’additivité des tensions : E = uL(t) + uR’(t)
en notant uL(t) la tension aux bornes de la bobine.
Or : uL(t) = r.i(t) + L.
di
dt
Et d’après la loi d’Ohm : uR’(t) = R’.i(t)
Donc : E = r.i(t) + L.
di
dt
+ R’.i(t)
Finalement : E = L.
di
dt
+ (R’ + r).i(t)
4. En régime permanent, i(t) = IP = Cte donc
di
dt
= 0. L’équation différentielle devient :
E = (r + R’).IP
5. E = r.IP + R’.IP
E – R’.IP = r.IP
r =
P
ER'
I
r =
3
4,0 10
290.10
= 4,0 / (2,90.102.10-3) -10
= 4,0/2,90 x 101 -10 = 1,4 x 101 -10
= 14 -10 = 4
6. La constante de temps est  = L/R
D’après la loi d’Ohm : [R]=[U].[I]-1
D’après le loi de la bobine (uL =L.di/dt) : [L]=[U].[T].[I]-1
Donc [L].[R]-1= [U].[T].[I]-1.[U] -1.[I]=[T]
La relation est bien homogène.
i(mA)
t(ms)
0
4,0
9
uL
IP = 290 mA