Page 1 sur 15 Elaboration et propriétés de matériaux métalliques

Page 1 sur 17
Elaboration et propriétés de matériaux métalliques - Option PC - Chapitre 1/4
Oxydo-réduction par voie sèche
Diagrammes d'Ellingham
Introduction :
• Dans l'industrie métallurgique, on utilise des réactions d'oxydo-réduction sans solvant, pour
préparer des métaux à partir des oxydes métalliques. Ce sont des réactions redox par voie
sèche.
L'oxydant responsable de l'apparition des oxydes métalliques est O2(g).
Par exemple : Na2O(s) Al2O3(s) Fe2O3(s) etc ...
• L'outil le plus adapté pour comprendre et prévoir les réactions chimiques associées aux
phénomènes redox par voie sèche est l'utilisation des diagrammes d'Ellingham.
• On appliquera les concepts présentés à la pyrométallurgie du zinc.
I Construction des diagrammes d'Ellingham :
1. Formation d'un oxyde :
On considère les réactions de formation des oxydes. Par exemple :
4 Na(s) + 1 O2(g) 2 Na2O(s)
4
3
Al(s) + 1 O2(g)
2
3
Al2O3(s)
Rem Toutes ces réactions sont écrites avec un coefficient stœchiométrique 1 devant O2(g), pour
que ces réactions puissent être comparées entre elles par la suite.
On peut aussi trouver une convention différente dans les énoncés : par exemple, écrire
toutes les réactions équilibrées avec
1
2
O2(g).
De manière générale, je symboliserai ces réactions sous une forme symbolique :
2 M + O2(g) 2 MO
On a l'habitude de parler également de " couple MO / M ".
Ces réactions sont de véritables réactions chimiques. On peut donc leur associer une
enthalpie standard de réaction : rG°(T).
On a bien évidemment rG°(T) = rH°(T) - T.rS°(T).
On constate expérimentalement que rG°(T) et rG°(T) sont quasiment indépendantes de
la température. Cela signifie que ces réactions chimiques sont étudiables sous
l'approximation d'Ellingham : rH° indépendant de T  rC°P = 0

Page 2 sur 17
 rS° est indépendant
de T
En résumé : 2 M + O2(g) 2 MO rC°P = 0
rG°(T) = rH°(T) - T.rS°(T) ≈ rH°(298) - T.rS°(298).
     rG°(T) = f) correspond donc à des portions de droite.
Ces tracés sont les diagrammes d'Ellingham :
Rem Sur ce diagramme, on remarquera l'unité inhabituelle pour rG°(T) : kJ.(mol.O2)-1, au lieu
de kJ.mol-1. Cela signifie donc que les réaction ont été écrites conventionnellement avec 1
O2(g) échangé, et que rG°(T) est exprimé en kJ.mol-1. Si on avait équilibré les réactions
chimiques avec
1
2
O2(g), on aurait écrit rG°(T) en kJ.(mol.
1
2
O2(g))-1. Dans le cas général,
il est conseillé de bien lire la convention utilisée dans l'énoncé.
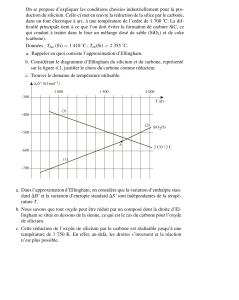
2. Commentaires sur le tracé :
a. Stabilité comparée des oxydes
Pour la réaction 2 M + O2(g) 2 MO , on peut associer sa
constante d'équilibre K°(T), qui vérifie : rG°(T) = -
RT.LnK°(T).
Plus rG°(T) est négatif, plus K° est élevée, et donc plus l'oxyde
est stable.

Page 3 sur 17
Les métaux très réducteurs et les oxydes très stables sont donc trouvés dans le bas du
diagramme (Ca : calcium ; Mg : magnésium : Al : aluminium ; Ti : titane).
b. Signe des pentes
Les pentes sont le plus souvent positives, car le plus souvent, les réactions sont écrites
avec M et MO en phases condensées (liquide, ou solide).
2 M(phase condensée) + O2(g) 2 MO(phase condensée)
Pour ce type de réaction :
◊ pente de rG°(T) : - rS°(298)
 pente positive
◊
i
i gaz
 1 rS(298)0
Contre exemple : CO(g) / C(gr)
2 C(gr) + O2(g) 2 CO(g)
◊ pente de rG°(T) : - rS°(298)
 pente négative (visible sur le diagramme)
◊
i
i gaz
 1 rS(298)0
c. Discontinuité des pentes aux températures de changement d'état pour M ou MO
On raisonne sur un exemple : on note TF la température de fusion de M. On désire montrer
que la pente du diagramme d'Ellingham pour T < TF (lorsque M est solide) est différente de
la pente pour T > TF (lorsque M est liquide). Sans perte de généralité, on prendra MO
solide.
On a donc : T = TF- : couple MO(s) / M(s)
T = TF+ : couple MO(s) / M(l)
2 M(s) + O2(g) 2 MO(s) rS°1

Page 4 sur 17
2 M(l) 2 M(s) rS°2
2 M(l) + O2(g) 2 MO(s) rS°3
La loio de Hess impose que rS°3 = rS°1 + rS°2
= rS°1 + 2.solidificationS°(M)
= rS°1 - 2.fusionS°(M)
= rS°1 - 2.
fusionH(M)
Tfusion(M)
Donc : pente (T>TF) = - rS°3
= - rS°1 + 2.
fusionH(M)
Tfusion(M)
= pente (T<TF) +
2.
fusionH(M)
Tfusion(M)
Donc : pente (T>TF) > pente (T<TF)
Rem La rupture de pente aurait été plus importante lors d'un changement d'état liquide / gaz, car
ébullitionS°(M) > fusionS°(M).
Exemple : rupture de pente autour de la
température de fusion du zinc pour le couple
ZnO(s) / Zn [point F] et autour de la température
d'ébullition du zinc [point E]
3. Domaines de stabilité de MO ou M :
On désire étudier dans un premier temps l'équilibre
2 M + O2(g) 2 MO rG°(T)
avec les méthodes classiques de la thermodynamique. On va distinguer le raisonnement
selon la nature des phases de M ou MO.
a. Cas où MO et M sont en phases condensées non miscibles :
On a donc, d'après nos hypothèses, a(MO) = 1 et a(M) = 1, car M et MO sont en phase
condensée pure.
On peut calculer la variance associée à l'équilibre, grâce à la formule de Gibbs :
v = k - q - r + n -  = 3 - 1 - 0 + 2 - 3 = 1
On peut alors utiliser la monovariance du système sous deux angles :
• Si on fixe T, alors PO2(éq) est fixée. Cela est d'ailleurs évident, car
rG°(T) = - RT.Ln(K°(T)) = - RT.Ln
P
PO2(éq)
= RT.Ln
PO2(éq)
P

Page 5 sur 17
• Si on fixe T et PO2 ≠ PO2(éq), alors il y aura évolution du système jusqu'à disparition de
l'une des phases (M ou MO). Il y a rupture d'équilibre. Cela est visible en exprimant
l'affinité chimique de la réaction :
A = RT.Ln
K(T)
Q
= RT.Ln
P
PO2(éq)
.PO2
P
= RT.Ln
PO2
PO2(éq)
2 M + O2(g) 2 MO A = RT.Ln
PO2
PO2(éq)
◊ Si PO2 > PO2(éq) alors A > 0. La réaction est totale dans le sens
direct.
Il y a évolution jusqu'à disparition
de M.
C'est le domaine de stabilité de
MO.
◊ Si PO2 < PO2(éq) alors A < 0. La réaction est totale dans le sens
indirect.
Il y a évolution jusqu'à disparition
de MO.
C'est le domaine de stabilité de M.
AN PO2(éq) est de l'ordre de grandeur de 10-20 bar. Sous la pression atmosphérique, on a
environ PO2 ≈ 0,2 bar. On est donc très souvent dans le cas où A > 0 (stabilité des oxydes).
On peut résumer ces résultats sur un diagramme traçant RT.Ln
PO2
P
= f(T) :
RT.Ln
PO2
P
T
PO2(éq )
P
RT.Ln
T
Stabilit é de M
(existence exclusive)
Stabilit é de MO
(existence exclusive) Equilibre MO / M
b. Si M et/ou MO ne sont pas d'activité 1 :
Traitons le cas où M est gazeux, et MO solide.
2 M(g) + O2(g) 2 MO(s) rG°(T)