BEP - Mathématiques et sciences physiques

1
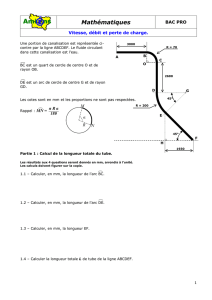
Une portion de canalisation est représentée ci-
contre par la ligne ABCDEF. Le fluide circulant
dans cette canalisation est l'eau.
BC est un quart de cercle de centre O et de
rayon OB.
DE est un arc de cercle de centre G et de rayon
GD.
Les cotes sont en mm et les proportions ne sont pas respectées.
Rappel : MN =
180α Rπ
Partie 1 : Calcul de la longueur totale du tube.
Les résultats aux 4 questions seront donnés en mm, arrondis à l'unité.
Les calculs doivent figurer sur la copie.
1.1 – Calculer, en mm, la longueur de l'arc BC.
1.2 – Calculer, en mm, la longueur de l'arc DE.
1.3 – Calculer, en mm, la longueur EF.
1.4 – Calculer la longueur totale L de tube de la ligne ABCDEF.
Mathématiques
BEP
Vitesse, débit et perte de charge.
A
B
C
D
E
F
G
H
O
3000
2600
1930
45°
45°
R = 70
R = 200
Ami ns
α
R
M
N

2
Partie 2 : Vitesse de l'eau dans la canalisation.
La vitesse v de l'eau dans la canalisation est donnée par la relation
S
Q
v 
Q : débit d'eau dans la canalisation S : aire de la section du tube
Si Q en m3/s et S en m², alors v en m/s
2.1 – Le diamètre intérieur du tube est D = 20 mm.
Compléter: D = 20 mm = …………… m.
2.2 – Montrer que l'aire de la section du tube est S = 3,14 x 10-4 m².
Prendre pour  la valeur approchée 3,14. Détailler les calculs.
2.3 – Le débit d'eau dans la canalisation est Q = 2,5 x 10-4 m3/s. Calculer, en m/s, la vitesse v de
l'eau dans la canalisation. Donner le résultat arrondi à 10-1. Détailler les calculs.
Partie 3 : Les pertes de charge – Utilisation de l'abaque de Dariès.
Dans une canalisation (de section constante) dans laquelle circule un fluide
(de l'eau par exemple), le frottement de ce fluide sur les parois provoque
des pertes de charge, c'est-à-dire une diminution de pression. Elles sont
exprimées en "mètre de conduite d'eau" (mCE) ou en "pascal" (Pa).
Il existe deux sortes de pertes de charge :
- Les pertes de charge linéaires (tube droit)
- Les pertes de charge dites accidentelles (coudes dans le cas qui nous concerne). Pour faire les
calculs elles sont données en équivalent de tube droit.
En page 3 figure l'abaque de Dariès. Dans cet abaque sont tracées 4 "axes logarithmiques"
correspondant chacun à une grandeur.
- Le débit Q.
- Le diamètre du tube D.
- La perte de charge par mètre p.
- La vitesse v.
3.1 – Sachant que 1 m3 = 1 000 L, Compléter:
Q = 2,5 x 10-4 m3/s = 2,5 x 10…… L/s = ……….. L/s

3
3.2 – Sur l'axe "débit Q " placer le point M tel que Q = 0,25 L/s
3.3 – Sur l'axe "diamètre D " placer le point N tel que D = 0,02 m
3.4 – Tracer la droite (MN) passant par ces deux points.
3.5 – Relever sur l'abaque la vitesse v de l'eau et la perte de charge par mètre p en tenant
compte de la présence de coudes.
Compléter: v = ……………………. m/s p = ……………………… m
3.6 – On considère que la longueur de tube de la portion de canalisation est L = 8,6 m.
Les deux coudes correspondent à une perte de charge supplémentaire équivalente à une
longueur de 1,5 m de tube droit.
En utilisant le résultat de la question 3.5 calculer la perte de charge totale PT (en mètre de
conduite d'eau) dans cette canalisation.
Abaque de DARIÈS
EMPLOI DE L'ABAQUE :
Connaissant deux éléments, on joint les points représentant ces
valeurs de ces éléments sur leurs axes verticaux. Les deux autres
éléments se lisent aux intersections de la droite avec les axes
correspondants.
Exemple : (voir droite tracée)
Pour un débit de 1,05 L/s et un diamètre intérieur de 26 mm, on lit :
perte de charge = 0,35 m par mètre et vitesse = 2 m/s
Cet axe donne des
valeurs supérieures
de 15 pour tenir
compte des pertes
de charge locales
telles que : coudes,
empattements et
robinets d'arrêt
situés sur la
conduite.
Les valeurs portées
sur cet axe ne
tiennent pas
compte des pertes
de charge locales.

4
Partie 4 : Les pertes de charge – Utilisation d'une formule.
Les pertes de charge se déterminent à l'aide de la relation suivante : Pc =
2D
v²ρ λ
avec : Pc: perte de charge (en Pa)
λ : coefficient de perte de charge linéique.
ρ : masse volumique du fluide (en kg/m3)
v : vitesse d'écoulement du fluide (en m/s)
D : diamètre intérieur du tube (en m)
4.1 - Dire si les affirmations suivantes sont vraies :
a) La perte de charge est proportionnelle à la masse volumique du fluide : ………………
b) La perte de charge est proportionnelle à la vitesse du fluide : ………………
c) La perte de charge est proportionnelle au diamètre intérieur du tube : ………………
4.2 – On donne D = 1,6 x 10-2 m et ρ = 1000 kg/m3
Calculer, en pascal (Pa), la perte de charge lorsque λ = 0,0225 et v = 0,8 m/s
Détailler les calculs.
4.3 – Calculer le coefficient de perte de charge linéique lorsque Pc = 633 Pa et v = 0,9 m/s.
Arrondir le résultat à 10-3. Détailler les calculs.
4.4 – Calculer, en m/s, la vitesse d'écoulement lorsque λ = 0,022 et Pc = 337 Pa.
Arrondir le résultat à 10-1. Détailler les calculs.
Partie 5 : Modélisation mathématique.
Pour λ = 0,0225 ; ρ = 1000 kg/m3 et D = 16 mm on peut écrire la relation sous la forme
Pc = 687,5 v²
Pour étudier l'évolution de la perte de charge en fonction de la vitesse d'écoulement du fluide,
on associe à la relation la fonction f de la variable réelle x définie sur l'intervalle [0 ; 14] par :
f(x) = 687,5 x²
5.1 – Compléter le tableau de valeurs.
x
0
0,2
0,4
0,6
0,8
1,0
1,2
1,4
f(x)
0
110
687,5
1347,5
5.2 – Dans le plan rapporté au repère orthogonal donné (page 5), tracer la représentation
graphique de la fonction f.
5.3 – Par lecture graphique, en laissant apparents les traits de construction nécessaires,
proposer :
a) la valeur de f(x) pour x = 0.65 : ………………..
b) la valeur de x pour laquelle f(x) = 830 : …………………..

5
5.4 – Répondre à l'aide d'une phrase à chaque question suivante :
a) Quelle est la perte de charge lorsque la vitesse d'écoulement est de 0,65 m/s ?
…………………………………………………………………………………………………………………………
b) Comment évolue la perte de charge lorsqu'on double la vitesse d'écoulement ?
…………………………………………………………………………………………………………………………
O
0,1
0,5
1,0
1,5
100
500
1000
1500
f(x)
x