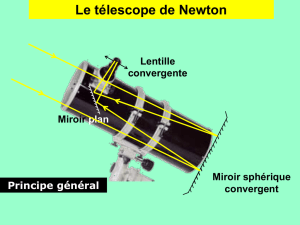
Le télescope de Newton (2):

Correction : le télescope de Newton
I. Images d'un objet réel AB dans un miroir plan et un miroir
sphérique
a. Pour obtenir l'image A'B' de la flèche AB, on construit son
symétrique par rapport au plan du miroir.
γ =
AB
BA ''
=1
b. Si l'objet AB est situé à l'infini sur l'axe , son image se forme dans le
plan focal image du miroir sphérique.
c. Dans cette question, l'objet AB n'est pas à l'infini.

II. Étude du télescope
a. (voir annexe en fin de corrigé)
L'image F1' de F1 par le miroir plan correspond au symétrique de F1 par
rapport au miroir plan. Alors IF1 = IF1'
L'objet AB est à l'infini. Le miroir sphérique en donne une image
intermédiaire A1B1 située dans son plan focal image. Le miroir plan en
donne une image A2B2 symétrique de A1B1 par rapport à ce miroir. Le
télescope est afocal. A2B2 est donc située dans le plan focal objet de
l'oculaire. L'image finale A'B' est à l'infini.
b. Le diamètre apparent est l'angle  sous lequel l'objet est vu à l'œil nu.
θ est l'angle entre AS et BS.
 est l'angle entre l'axe  et AS mais aussi l'angle entre  et BS.
On a donc  = 2 
c.
A∞ étant à l'infini, son image A1 donnée par le miroir sphérique est dans
son plan focal image.
Remarque :
Ici, il vaut mieux éviter de déterminer l'image de A en cherchant
l'intersection des rayons suivants :

- le rayon issu de A , parallèle à l'axe optique, réfléchi par le miroir
et passant par F1.
- le rayon issu de A, passant par F1 et réfléchi par le miroir
parallèlement à son axe optique.
En effet, l'image trouvée n'est pas alors dans le plan focal image du miroir.
Ceci est dû au fait que le schéma est fait en plaçant l'objet à distance finie.
Si l'on recule progressivement l'objet, le deuxième rayon est de moins en
moins incliné par rapport à l'axe optique. L'intersection des deux rayons se
produit alors de plus en plus près du plan focal image du miroir sphérique.
d. Le point B situé à l'infini (symétrique du point A par rapport à Δ) à pour
image le point B1 symétrique de A1 par rapport à F, conformément au
schéma ci-dessus.
α (rad) ≈ tanα =
1
11 )
2
(
f
BA
θ (rad) = 2α =
1
11
fBA
e. A2 est le symétrique de A1 par rapport au plan du miroir. De même, B2
est le symétrique de B1 par rapport au plan du miroir .
D'où A2B2 = A1B1
A2B2 = A1B1 =  f1 = 0,00872 x 1,20 = 1,05.10-2 m = 1,05 cm
f. AB étant à l'infini, A1B1 est dans le plan focal image du miroir
sphérique.
Pour disposer A2 et B2 , on prend les symétriques de A1 et B1 par rapport
au miroir plan.
L'objet A2B2 étant dans le plan focal objet de l'oculaire, l'image finale de la
Lune est à l'infini.
B2
A2
O2
F2
F'2
L2
'
Bfinal
Afinal
'

g. α' (rad) ≈ tan ' =
22
22OF FA
=
'
2
22 )
2
(
f
BA
d'où 2 ' 
'
2
22
f
BA
A1B1   f1  2  f1  A2B2 2  f1 = 2 '
'
2
f
α' =
'
2
1
.
f
f
h. Considérons les rayons suivants :
- le rayon issu de A2 et passant par O2
- le rayon issu de B2 et passant par O2
Ces rayons définissent l'angle B'O2A' = 2α' = θ' qui est l'angle sous lequel
l'observateur voit l'image finale.
i.
'
2
1
'' f
f
=
2
10.00,2 20,1
= 60,0
Ce rapport représente grossissement du télescope. Le télescope agrandit 60
fois par rapport à la vision à l'œil nu.