Four solaire

Four solaire
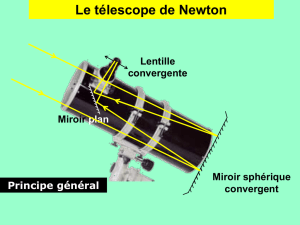
1) Quand la parabole est orientée vers le soleil les rayons du soleil convergent vers le foyer
du four.
Le four ressemble à un miroir sphérique . son foyer est situer à R/2.
Remarque : Seuls les rayons proches de l'axe optique convergent au foyer ( approximation de
gauss) , les autres sont un peu éloignés du foyer.
2) Si D est le diamètre du four, la surface qui reçoit les rayon est de
S=π D²
4
Pour D=1.2 m S=1.13 m² d'ou une puissance de 1.13 KW.

L’objet étant situé à l’infini, l’image se situe dans le plan focal du miroir. Pour un miroir le
point focal est placé au milieu de C1S1
F1S1=C1S1
2
.
A1B1=αC1F1
On sait que : si l’angle est petit et exprimé en radians, nous obtenons
:
A1B1=α C1S1
2=9mm
Si on veut tenir compte de l'orientation de l'image sur l'axe
perpendiculaire à l'axe optique
A1B1<0
;l'image est à l'envers.
L’image finale A'B' étant à l’infini, l’image A2B2 est au foyer objet de l’oculaire (Lentille de
point focal
F
) .
(
AB
∞
)
(
M1
⇒
)
(
A1B1
F1
)
(
M2
⇒
)
(
A2B2
F delalentille L
)
(
Oculaire
⇒
)
(
A ' B'
∞
)
Le miroir M2 donne de A1B1 une image A2B2 symétrique de A1B1 par rapport au plan du miroir
M2. Donc A2B2 est parallèle et se sens opposé à l’axe optique du miroir M1 .

D’après les propriétés de symétrie on a :
F1S2=S2F=y−f
(f étant la distance focale de l’oculaire).
S2S1=F1S1−F1S2=C1S1
2−( y−f)
On sait que
f=1
V=2cm⇒S2S1=90 cm
Application numérique:
D’après les propriétés de symétrie on a :
A2B2=A1B1
, et
A1B1<0
donc
α'=A2B2
f=A1B1
f=−α C1S1
2f =−0.45rad≈−25 °47'
On a donc :
α'
α=−C1S1
2f =−50
le signe – veut dire que l'image est renversée.

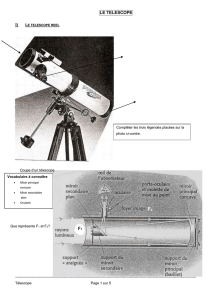
Télescope à deux miroirs
Szőcs Tamás Tamasflex
L'objet AB est à l'infini, son image
A1B1
est au foyer image
F1
du miroir M1; la
relation de conjugaison du miroir sphèrique est :
1
S1A+1
S1F1
=2
S1C1
⇒S1F1=S1C1
2
Cette image devient un objet (situé à la distance
S2F1
) pour le miroir M2. On veut que
l'image donnée par M2 soit sur S1. La relation de conjugaison devient :
1
S2F1
+1
S2S1
=2
S2C2
or
S2F1=S2S1+S1F1
 6
6
1
/
6
100%