CULTURE GENERALE CRYPTOGRAPHIE Plan Pourquoi un cours

1
CULTURE GENERALE
CRYPTOGRAPHIE
Plan
Pourquoi un cours consacré à la cryptographie ?
La stéganographie : Art du camouflage
La transposition
La substitution
L’étude des fréquences
Le chiffre de Marie Stuart
Le secret du masque de fer
La substitution homophonique
Le chiffre indéchiffrable
 Pourquoi un cours de cryptographie ?
Le pharmacien expert en écritures
 L’Officine de Dorvault (1844) fait du pharmacien un expert en écritures publiques et privées, apte à détecter
falsifications et encres sympathiques
 L’art des cryptanalystes
Une illustration ludique du discours de la méthode
 La stéganographie : Art du camouflage (Dissimulation même du message)
Les premiers témoignages
 Les histoires d’Hérodote, témoignages sur les guerres médiques
. Xerxès et les tablettes de cire de Demaratus
(Xerxès prépare un armée pendant 5 ans afin d’envahir la grande cité Grecques en secret. Demaratus découvre le
plan de Xerxès et envoi un messager à Sparte afin de les préparer à la défense. Le messager prit l’apparence d’un
petit commerçant. Il porte un message mais il ignore ce qu’il est. Le messager subit un contrôle lorsqu’il franchi la
frontière mais les contrôleurs ne trouve rien, il est porteur de tablettes où le message est caché sur le bois)
 Le rasoir d’Histaïaeus
 L’œuf dur de Giovanni Porta
(Le message est écrit sur la coquille de l’œuf dure et sera lisible sur le blanc de l’œuf)
Sous d’autres latitudes
 Les boulettes de cire chinoise
(Boulettes de soies avalées par le messager)
Les jeux littéraires
 L’abjuration d’un catholique
 George Sand à Alfred de Musset
 La transposition (Rendre le message incompréhensible)
Le principe
 Une redistribution des lettres du message
 Ceci conduit à une anagramme
 Exemple : OPIRE conduit à 2 possibilités de texte en clair
POIRE et PROIE
 La nécessité d’une clé pour coder et décrypter
 L’écriture en dent de scie
Ton secret est ton prisonnier : S’il fuit tu deviendras son prisonnier
 La scytale spartiate
(On enroule un ruban de cuir autour d’un scytale (bâton hexagonale))

2
Le principe de base de la cryptographie
 Tout cryptage repose sur un principe (Algorithme) et une clé
 La clé prime sur l’algorithme en termes de sécurité
 « La sécurité d’un système de cryptement ne doit pas dépendre de la préservation du secret de l’algorithme. La
sécurité ne repose que sur le secret de la clé » Auguste Kerchoffs Van Nieuwenhof, La cryptographie militaire,
1883
 La substitution (Coder un message)
Le principe
 Le remplacement d’une lettre du texte clair par un signe quelconque (Autre lettre, chiffre…)
 Exemples
 Le chiffre Pigpen (Francs-maçons, XVIIIe siècle)
 Le chiffre des templiers
 Le chiffre du Kama Sutra
A D H I K M O R S U W Y Z
V X B G J C Q L N E F P T
L’exemple historique : Le chiffre de César
 La Guerre des Gaules
 La vie des douze Césars de Suétone
 Un décalage de trois rangs dans l’alphabet
Exemple : Veni Vidi Vici
YHQL YLGL YLFL
 La faiblesse de ce chiffre
Le nombre limité de clés (25) d’où
La substitution avec mot-clé
Julius Caesar
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
J U L I S C A E R T V W X Y Z B D F G H K M N O P Q
L’apport de la civilisation arabe
 IXe siècle : l’âge d’or d’une civilisation (Mathématiques, linguistique, étymologie…)
 Abu Yusuf Ya’qub ibn as-Sabbath ibn Oomran ibn Ismail al-Kindi
 Le manuscrit sur le déchiffrement des messages cryptographiques
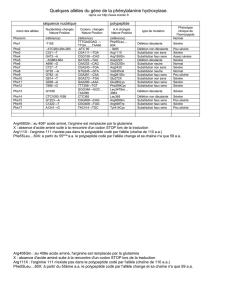
 L’analyse des fréquences
 L’outil de base de la cryptanalyse
(Fréquences des lettres dans différentes langues
Lettre %
A 9,42%
B 1,02 %
C 2,64 %
D 3,39 %
E 15,87 %
…
K 0,00 %
W 0,00 %
(La méthode par substitution par mots clés peuvent être déchiffrés par l’analyse de la fréquence)
Les premiers cryptanalystes occidentaux
 Giovanni Soro
 Philibert Babou
 François Viète
(Réussi à décrypter les écritures secrètes de Philippe II, dit inviolable)

3
Les tentatives d’amélioration du chiffre de substitution
 Introduction de diversions cryptographiques (Signes nuls, doublés…)
 Ajout de mots de code (Notion de Nomenclature)
Synthèse générale
Stéganographie
(Cachée)
Ecriture
Secrète Code
Substitution
(Cryptographie
(Brouillé) Chiffre
Transposition (Change les lettres)
 Le chiffre de Marie Stuart
 Une petite reine en exil
 Décembre 1542 naissance de Marie
 1548 Départ pour la France
 1558 Mariage avec le dauphin François
 (Marie devient reine de France et reine d’Ecosse. Mort de François elle devient veuve à 18 ans)
 1561 Retour en Ecosse
 Marie reine d’Ecosse
 Un peuple en majorité presbytérien
 Une instabilité politique
 Des alliances désastreuses
 1568 La fuite en Angleterre
 19 ans d’emprisonnement
 Un danger pour Elisabeth
 Une détention de plus en plus dure
 … Mais un jour l’espoir !
 Le complot
 Le geôlier Gilbert Gifford
 La conjuration de Babington
 Walsingham et le linguiste Th. Phelippes
 1586 Ouverture de du procès
 Le faux post-scriptum
 Un chiffre imparfait
 Une substitution alphabétique renforcée par des mots-codes
(Marie ignore que Gifford est un traitre, Gifford travaille pour Walsingham, Phelippes un mathématicien qui sait
parler une dizaine de langue réussi à percer l’écriture secrète de Marie. Connaissant le cause Phelippes rajoute un
post-scriptum sur une lettre de Marie)
 Une fin héroïque
 Décapité le 8 février 1587
 Le secret du masque de Fer
 Le Grand chiffre de Louis XIV
 Elaboré par Antoine et Bonaventure Rossignol
 Inviolé jusqu’à la fin du XIXe siècle
 Etienne Bazeries

4
 Un chiffre d’un nouveau type
 587 nombres différents
 Apparaissant chacun des milliers de fois
 Un nombre codant pour une syllabe
 124 22 125 46 345
Les en ne mi s
 Le mystère dévoilé
 Un prisonnier masqué
 Incarcéré à Pignerol
 Décédé à la Bastille en 1703 après 37 ans de détention
 Vivien de Bulonde
 La substitution homophonique
 Une solution pour contrer l’analyse des fréquences
 Remplacer chaque lettre par différents substituts
 Le nombre de substituts est égal à la fréquence de la lettre
 Exemple : La fréquence du A en français = 9%
On utilise 9 symboles
 Chaque symbole du code possède une fréquence de 1%
 La faille : la « personnalité de chaque lettre »
 Les correspondances entre les lettres
 Exemple : Le Q est toujours suivi dans le corps d’un mot par un U
Q = 1% et U = 6%
Un même symbole toujours suivi des six même symboles = Q
 Le chiffre indéchiffrable
Le but recherché
Une lettre Un
En clair symbole
 Le chiffre parfait
 Blaise de Vigenère (1523-1596)
 Le traité des chiffres (1586)
 Le premier chiffre de substitution polyalphabétique
 Le carré de Vigenère
 26 alphabets chiffrés (Chiffre de César)
1 : A B C D … Z
2 : B C D E … A
3 : C D E F … B
4 : D E F G … C
 Un mot clé
 Pour définir l’alphabet utilisé
 Exemple : V I V E F O U A S S I E R
R o u g e r o u g e r o u
M W P K J I U Y W Z S L
 L’objectif est atteint
 S est code par Y et par W
 W code pour I ou S

5
 …Et les clés de son décryptage
 L’étonnant M. Babbage (1791-1871)
 Le précurseur de l’ordinateur
 La controverse avec le dentiste de Bristol
 L’application de la méthode
 Avoir des idées claires et distinctes
. Il existe autant de façon de coder un mot du texte clair qu’il y a des lettres dans la clé
c l e c = JAMR
N O T E
l e c l = GWIZ
e c l e = OVRO
. Dans un texte chiffré, si un même mot apparait plus de fois qu’il y a de lettres dans la clé, nous obtiendrons
des répétitions de suites de lettres identiques
 Analyse
. Diviser le problème
. La longueur du mot-clé
. Identifier les lettres du mot-clé
 Synthétiser
. Aller du plus simple au plus compliqué
. D’abord la longueur puis la lettre elle-même
 Découvrir la longueur du mot-clé
 S’attacher aux répétitions de groupes de lettres
 Identifier les lettres du mot-clé
 Reconstituer des messages artificiels codés par un seul alphabet
 Appliquer à chacun l’analyse des fréquences
 Dernière étape : Dénombrer
 A-t-on négligé quelque chose ?
 Le rôle du hasard dans les répétitions de lettres
 Ne retenir que les groupes d’au moins quatre lettres
Questions :
1. Expliquer en quoi la philosophie de Démocrite constitue une première tentative d’explication matérialisme du
vivant ?
2. Comment Parménide et Héraclite s’oppose t-il pour expliquer la diversité du vivant ?
3. Pourquoi peut-on dire que la philosophie des Sophistes représente une rupture par rapport au philosophe de la
nature ?
4. Expliquer en quoi la philosophie de Platon est annonciatrice d’une certaine métaphysique ?
5. Dans quel mesure peut-on affirmer qu’Aristote à Rompu avec la métaphysique de son maitre Platon ?
6. Exposer les grandes lignes de la philosophie des Stoïciens
7. Quel est la méthode prônant par Descartes pour atteindre toute vérité en menant correctement son
raisonnement
8. Comment les philosophes tenants du métaréalisme en sont ils venu à conclure que l’observateur créait le réel ?
9. En quoi le décryptage du chiffre de Vigenère par Babbage constitue t-il une application du discours de la
méthode ?
10. Jusqu’au 17e siècle quelles étaient les principales techniques de cryptage d’un message ?