Etude expérimentale d`une bobine 6pts

Correction : TERMINALES S – DS n°4
Exercice 1 : Etude expérimentale d’une bobine ( 10 points ) ( 55 minutes )
1 - Détermination expérimentale de l'inductance L de la bobine
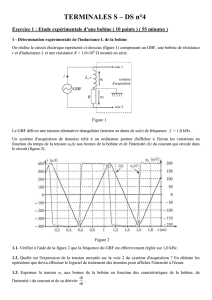
On réalise le circuit électrique représenté ci-dessous (figure 1) comprenant un GBF, une bobine de résistance
r et d'inductance L et une résistance R = 1,0104  montés en série.
Le GBF délivre une tension alternative triangulaire (tension en dents de scie) de fréquence f = 1,0 kHz .
Un système d'acquisition de données relié à un ordinateur permet d'afficher à l'écran les variations en
fonction du temps de la tension uL(t) aux bornes de la bobine et de l'intensité i(t) du courant qui circule dans
le circuit (figure 2).
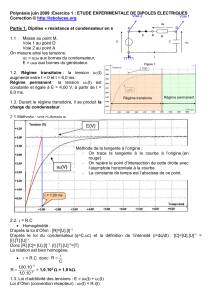
1.1. Vérifier à l'aide de la figure 2 que la fréquence du GBF est effectivement réglée sur 1,0 kHz.
Le GBF délivre une tension alternative triangulaire: le courant i(t) qui circule dans le circuit est triangulaire.
Entre les points C et B du graphe i(t) on a une période de i(t) telle que :
T = 1,6 – 0,60 = 1,0 ms =1,010–3 s.
Or la fréquence f est reliée à T par: f =
1
T
R
L, r
u1
u2
GBF
i
voie 1
voie 2
Figure 1
système
d'acquisition
Figure 2

donc: f =
3
1
1,0 10
= 1,0103 Hz = 1,0 kHz.
( 1 : 0,5 pour T puis 0,5 pour f )
1.2. Quelle est l'expression de la tension mesurée sur la voie 2 du système d'acquisition ? En déduire les
opérations que devra effectuer le logiciel de traitement des données pour afficher l'intensité à l'écran.
Compte tenu du sens du courant choisi, la loi d'Ohm donne : u2 = – R.i
Pour afficher l'intensité i à l'écran, il faut créer une nouvelle variable définie par i = – u2 / R.
On indiquera au logiciel de traitement des données i = – (u2 / 1,0104 ) .
( 0,5 )
1.3. Exprimer la tension uL aux bornes de la bobine en fonction des caractéristiques de la bobine, de
l'intensité i du courant et de sa dérivée
dt
di
.
La tension uL aux bornes de la bobine est égale à la tension u1. Compte tenu du sens du courant on a:
uL = r.i + L.
dt
di
( 0,5 )
1.4.1. Sur la figure 2, la représentation graphique de la fonction i(t) montre qu'en réalité, les crêtes de
l'intensité sont arrondies. Dans ces conditions, la tangente au sommet est horizontale.
En déduire une expression simplifiée de uL quand l'intensité dans le circuit est extrémale.
Quand l'intensité dans le circuit est extrémale le terme
dt
di
est nul et donc: uL = r.i.
( 0,5 )
A la lecture de i(t) pour t = 1,6 ms, que peut-on dire de r ?
Par lecture, on observe que uL  0 V pour t=1,6 ms donc r est très faible.
( 0,5 )
1.5. On néglige dans la suite le terme faisant intervenir r dans l'expression de uL ainsi que les arrondis des
crêtes de l'intensité.
À partir de la demi-période comprise entre les points C et D de la figure 2, mesurer uL , calculer
dt
di
et en
déduire la valeur de L.
Entre les points C et D, on mesure: uL = 0,200 V . (attention échelle à droite)
D'autre part:
dt
di
ii
i
t t t
DC
DC
dt
di
__
_ _ 6 4
__
_ 3 3
[400 ( 400)] 10 8,00 10
(1,1 0,6) 10 0,5 10
= 1,6 A.s–1 (avec 2 chiffres significatifs.)
( 1 valeur et unité )
On néglige le terme faisant intervenir r dans l'expression de uL donc: uL = L.
dt
di
On en déduit donc la valeur de L, L = uL /
dt
di
L =
0,200
1,6
= 0,125 H = 0,13 H
( 0,5 )
2 - Constante de temps d'un circuit RL

En réalité, la valeur de r est de 12 .
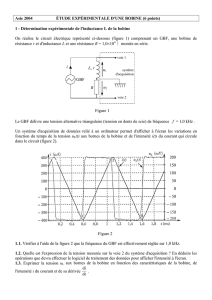
La bobine est maintenant montée en série avec une résistance R' = 100  aux bornes d'un générateur idéal de
tension de f.e.m. E = 6,5 V (figure 3).
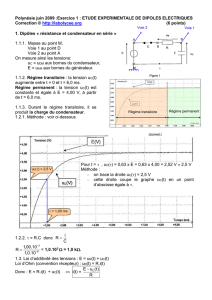
Le système d'acquisition permet de suivre l'évolution de l'intensité du courant dans le circuit en fonction du
temps. La fermeture de l'interrupteur à l'instant t = 0 déclenche l'acquisition. L'enregistrement obtenu est
représenté sur la figure 4.
R'
L, r
K
u
i
système
d'acquisition
de données
Figure 3
E
(ms)
t
0
1
2
3
4
5
6
7
i(t)
(mA)
10
20
30
40
50
60
I en régime permanent
Figure 4

2.1. Établir l'expression donnant l'intensité du courant en régime permanent en fonction des caractéristiques
du circuit.
La loi d'additivité des tensions donne: E = uL + u
E = r.i + L.
dt
di
+ R'.i
En régime permanent, l'intensité du courant est constante (donc
dt
di
= 0 ) et égale à sa valeur maximale notée
I.
( 0,5 )
L'expression précédente devient E = r.I + R'.I
E = (r + R').I
Donc: I =
)'Rr( E +
( 1 )
2.2. Vérifier que la valeur de l'intensité du courant en régime permanent obtenue sur le graphe de la
figure 4 est en accord avec les données de l'énoncé.
Graphiquement, sur la figure 4, pour le régime permanent, on lit I légèrement inférieure à 60 mA.
Par le calcul on a: I =
6,5
(12 100)
= 5,8.10-2 A = 58 mA
Les deux valeurs sont donc en accord.
( 1 )
2.3.1. Rappeler l'expression de la constante de temps d'un dipôle RL.
La constante de temps du circuit RL est :  =
Totale
L
R
=
'
L
Rr
( 0,5 )
2.3.2. Déterminer graphiquement sa valeur en faisant figurer la méthode utilisée sur la figure 5 en annexe à
rendre avec la copie.
On peut déterminer graphiquement la valeur de  en utilisant la méthode de la tangente à l'origine: la tangente
à l'origine coupe l'asymptote horizontale I = 58 mA en un point d'abscisse t = .
On lit:  = 1,1 ms.
( 0,5 )
i(t)
(mA)
10
20
30
40
50
60
I en régime permanent

remarque:
En utilisant la constante de temps du circuit RL :
 = L / (r + R') = 0,125 / 112 = 1,116.10-3 s  1,1 ms (avec valeur de L calculée au 1.5. non arrondie)
On vérifie donc bien que les deux valeurs de  sont en accord.
2.4. La résistance R' est en réalité une résistance réglable. On lui donne maintenant la valeur 150 .
2.4.1. Calculer la nouvelle intensité du courant en régime permanent.
I ' =
)'Rr( E +
Avec R' = 150  : I' =
6,5
162
= 4,010–2 A = 40 mA.
( 0,5 )
2.4.2. Calculer la constante de temps du nouveau dipôle RL.
' =
'
L
Rr
' =
0,125
162
= 7,710–4 s = 0,77 ms
( 0,5 )
2.4.3. Représenter avec soin la courbe représentant l'évolution de l'intensité du courant en fonction du temps
i = f(t) sur la figure 5 en annexe, à rendre avec la copie.
Vous utiliserez une couleur différente pour cette nouvelle courbe et prendrez soin d’utiliser les calculs des
questions 2.4.1 et 2.4.2 .
( 1 :  et  ou  )
Afin de tracer la nouvelle courbe représentative de i=f(t), nous allons procéder ainsi:
 Tracer l'asymptote horizontale I ' = 40 mA,
 Placer le point de coordonnées (t = 5' = 3,9ms ; i = I' = 40 mA),
 Placer le point de coordonnées ( t = ' = 0,8 ms ; i = 0,63I' = 25 mA)
 Utiliser la tangente à l'origine déjà représentée sur la figure 5.
En effet l'expression théorique de i(t) est : i(t) =
()
E
Rr
. (1 – e–t/ ) ou i(t) =
()
E
Rr
–
()
E
Rr
.e–t/
La dérivée a pour expression
di
dt
= –
()
E
Rr
–
1
.e–t/
avec =
L
Rr
alors
di
dt
=
()
E
Rr
R+r
L
.e–t/
di
dt
=
E
L
.e–t/
Le coefficient directeur de la tangente à la courbe représentative de i=f(t) à la date t = 0 s a pour expression
:
0t
di
dt 
=
E
L
donc ce coefficient n'est pas modifié si seule la valeur de R change.