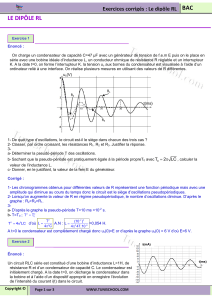
3) Remarque : entretien des oscillations du circuit (RT, L, C)

1
TSMP Cours Physique
Chap 6 : Les oscillations électriques libres d’un dipôle (RT, L, C)
Vous connaissez maintenant 3 dipôles électriques : le résistor, la bobine et le condensateur.
Nous allons dans ce chapitre associer ces trois composants en série de manière à constituer un
« dipôle RLC ou circuit RLC série ». La bobine et le condensateur étant capables de stocker
puis de redonner de l’énergie, nous nous intéresserons aux échanges énergétiques entre les
différents composants d’un tel dipôle qui peut se comporter comme un oscillateur électrique.
Les oscillations électriques sont omniprésentes dans notre vie quotidienne : celles-ci sont
utilisées en électronique pour les horloges des circuits numériques par exemple. Ainsi,
montres, téléphones portables, ordinateurs, chaînes audio et vidéo, appareils photo, caméras
vidéo numériques, four à micro-onde… tous ces « copains du quotidien » font appel à des
oscillations électriques pour fonctionner.
I. Oscillations électriques libres amorties d’un dipôle (RT, L, C) série
1) Etude expérimentale
Que deviennent la charge et la décharge d’un condensateur dans un circuit qui comporte une bobine ?
A l’oscilloscope, on observe :
Sur la voie A : la tension …………………………. qui
correspond à la tension aux bornes du …………………
mais aussi à la tension délivrée par le …………………..…
Sur la voie B : la tension ……………………………..…
aux bornes du …………………..……..
Conclusion :
La charge et la décharge d’un condensateur à travers un dipôle (RT,L,C)
ne sont pas …………………….……………. et donnent lieu à des
………………..…………………………………………. si la résistance R
est petite.
Rem 1 : les oscillations de tension observées ici sont …………………
puisqu’on laisse le circuit évoluer librement sans intervention extérieure
pendant la charge ou pendant la décharge.
Rem 2 : ces oscillations sont dues à la bobine qui tend à …………………………… à l’établissement des courants de charge et de
décharge par le phénomène d’auto-induction.
Rem 3 : les oscillations ne durent que le temps d’un régime ………………………… Ensuite s’installe le régime ………………….
Animation : http://www.sciences.univ-nantes.fr/physique/perso/gtulloue/Elec/Transitoire/Condensateur1_flash.htm
t
uGBF
0
UG
uGBF = UG = cte 0 : le
condensateur se charge
uGBF = 0 (GBF court-circuité) :
le condensateur se décharge
i
Y
A
GBF
B
Y
B
A
C
M
R petite
variable
(+)
(L, r)
dipôle (RT, L, C) :
le résistor, la
bobine et le
condensateur
sont en série
D

2
2) Les différents régimes
Augmentons progressivement la valeur de la résistance R et observons les modifications qui en résultent sur l’écran de
l’oscilloscope.
R = ……………..
R = ……………..
R = ……………..
Oscillations ………………………..
……………………………….
Oscillations ………………………..
……………………………….
………………………………………..
Régime ………………………………..
Régime ………………………………..
Régime ………………………………..
Conclusion :
L’amortissement des oscillations libres d’un dipôle (RT, L, C) est d’autant plus important que sa résistance totale
(ici RT = ……………..) est plus ………………………
Quand RT (ou R ici) augmente, on passe d’un régime ………………………………………….. (oscillations amorties) à un
régime ………………………………. (plus d’oscillations).
Rem : la valeur de RT pour laquelle on passe du régime pseudo-périodique au régime apériodique est appelée : « résistance totale
…………………… » RTC du dipôle.
Cette résistance ne peut dépendre que des deux autres caractéristiques physiques du dipôle à savoir L et C.
En utilisant des formules simples, déterminer la dimension du rapport
C
L
:
Ainsi, pour RT = RTC =
C
L
2
, on observe le régime apériodique pour lequel on atteint le
régime permanent le plus rapidement : on l’appelle régime ………………………..
Sur la figure de droite, tracer l’allure de la tension de charge du condensateur pour RT = RTC et
RT > RTC.
Animation : http://gilbert.gastebois.pagesperso-orange.fr/java/rlc/rlclib/rlc.html
t
uC
0
UG

3
II. Oscillations électriques libres non amorties d’un dipôle (L, C)
1) Amortissement des oscillations d’un circuit (RT, L, C) série
Voici un autre dispositif expérimental.
Le principe est le même que précédemment
mais on n’effectue ici qu’une seule charge du
condensateur et qu’une seule décharge car le
générateur est un générateur de tension
constante.
K2 restant ouvert, on ferme l’interrupteur
K1 : le condensateur se charge.
On ouvre K1 et on ferme K2, le condensateur
se décharge dans le dipôle (RT, L) selon un
régime pseudo-périodique ou apériodique
suivant la valeur de RT (donc de R).
On obtient :
Au départ, juste avant la décharge, i = …………. et uC = ………………. : l’énergie électromagnétique totale du circuit (RT, L, C)
vaut Ee = ……………. = ……………… (condensateur) + Em = ……………… = ………… (bobine) = ………… en tout.
A la fin de la décharge, i = …………. et uC = ………………. : l’énergie électromagnétique totale du circuit (RT, L, C) vaut
Ee = ……………. = ……………… (condensateur) + Em = ……………… = ………… (bobine) = ………… en tout.
Le circuit a donc perdu de l’énergie par effet Joule à cause de sa résistance électrique.
Conclusion : l’amortissement des oscillations libres d’un circuit (RT, L, C) série est dû aux transferts énergétiques par effet
Joule (à cause de RT) vers le milieu extérieur. L’énergie électromagnétique totale du circuit (RT, L, C) série diminue au cours
des oscillations qui s’amortissent.
Puisque l’amortissement des oscillations est dû à la résistance totale du dipôle, pour obtenir des oscillations non amorties, on a alors
deux possibilités :
Utiliser un circuit (L, C) de résistance totale nulle (RT = 0) : solution impossible en pratique car toute bobine ou même un
simple fil possède une résistance interne sauf les matériaux supraconducteurs (chers et peu pratique d’utilisation….).
Restituer continuellement au circuit l’énergie perdue grâce à un dispositif d’entretien des oscillations, comme par exemple
le montage à amplificateur opérationnel dit à « résistance négative » étudié plus loin.
Rem : les résultats sont tout-à-fait analogues à ceux caractérisant les oscillateurs mécaniques (pendules simple et élastique).
L’oscillateur étant ici le circuit électrique, l’énergie électromagnétique perdue ici par effet Joule à cause de la résistance électrique
du circuit correspondant à l’énergie mécanique perdue par chaleur à cause des frottements.
Animation : http://subaru2.univ-lemans.fr/enseignements/physique/02/electri/rlclibre.html
C
K1
Circuit de
décharge
UG = 6,0 V
Circuit de
charge
K2
R
(+)
A
uC
M
(L, r)
UG
UG
RT petite
régime pseudo-périodique
RT importante
régime apériodique
uC (t)
uC (t)

4
2) Entretien des oscillations
a) Principe
Le générateur fournit à ses bornes une tension proportionnelle au
courant qu’il délivre : uAM = k*i avec k > 0 coefficient ajustable.
Ecrire la loi d’additivité des tensions pour trouver l’équation
différentielle caractérisant le circuit :
Montrer que le générateur se comporte comme un dipôle de
« résistance négative » de valeur – k :
Réécrire l’équa-diff précédente dans le cas où k = RT = R + r et
représenter à droite le schéma électrique correspondant à un tel cas :
Conclusion : le circuit se comporte alors comme un dipôle
………….. de résistance totale ……………… Les oscillations
électriques correspondantes ne sont donc plus …………………….
Rem : représenter l’allure des oscillations que l’on observerait dans les 3 cas suivants :
a.1) K = RT a.2) K < RT a.3) K > RT
b) Dispositif à Amplificateur Opérationnel (A.O)
Un amplificateur opérationnel est un circuit intégré qui
permet d'amplifier une différence de potentiel
électrique présente à ses entrées + et .
Il a été initialement conçu pour effectuer des
opérations mathématiques sur des tensions dans les
calculateurs analogiques : addition, soustraction,
dérivation, intégration.
Il est alimenté par les bornes –15 V et +15V.
Ici, il est utilisé comme source de courants.
L’amplificateur opérationnel est supposé idéal et en
fonctionnement linéaire ce qui signifie :
i + = i
= 0 et V +- V - = uHI = 0
Dans ces conditions :
AO
+
−
R1
R1
R0
M
A
H
I
K
S
is
i -
i +
i ’
i
i
i
i ’
i ’
i ’
i + i ’= is
i
i
+ 15V
- 15V
i
B
A
C
M
R
(+)
G
(L, r)
D
Dipôle
(RT, L, C)

5
Rem : le dispositif d’entretien des oscillations compense les pertes par effet Joule dues à RT en fournissant à chaque instant au
circuit une énergie équivalente qui, dans le cas d’un dispositif à A.O est délivrée par ……………………………………………….
Pour en savoir plus sur l’AO : http://fr.wikipedia.org/wiki/Montages_de_base_de_l'amplificateur_opérationnel
3) Oscillations libres non amorties d’un circuit (L, C)
K2 restant ouvert, on ferme l’interrupteur
K1 : le condensateur se charge.
On ouvre K1 et on ferme K2, le condensateur
se décharge dans l’inductance pure (L) selon
un régime périodique.
On obtient :
Conclusion :
La décharge d’un condensateur dans une inductance pure produit des oscillations libres sinusoïdales …………………….
a) Etude de uC et de i
On montrera bientôt que uc(t) obéit à une équation différentielle dont la solution est
uc(t) = UCm*cos(
0t) avec UCm= ……………
T0 est la ………………………………………….. des oscillations (voir figure) et
0
est la ……………………………………….. du phénomène, définie l’année dernière
lors du chapitre sur les oscillateurs.
On avait vu que :
=
0
2
T
Son unité est donc …………
C’est un peu l’équivalent d’une « vitesse angulaire » pour un oscillateur…
A partir de la solution l’expression de uc(t), trouver celles de q(t) et de i(t) que l’on mettra sous la forme : q(t) = Qm*cos(
0t)
et i(t) = Im*cos(
0t + a). Donner les expressions de Qm de Im et de la constante a.
On constate que i(t) est en avance sur uc(t) de ……. ce qui correspond à ……………… On dit que i(t) est en …………………….
avance sur uc(t) ou que uc(t) est en …………………………. retard sur i(t).
C
K1
Circuit de
décharge
UG = 6,0 V
Circuit de
charge
K2
(+)
A
uC
M
(L, r = 0)
RT nulle
régime périodique
uC (t)
uC (t)
T0
UG
 6
6
 7
7
 8
8
1
/
8
100%