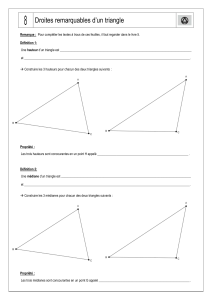
les triangles sont equilateraux

B
C
D
E
Pour ceux qui ont des difficultés je mets la solution ci-dessous,
mais cherchez un peu avant d’aller voir !!!!!
Paradoxe
Voici une démonstration basée sur des théorèmes justes et qui montre que tous les triangles sont équilatéraux !
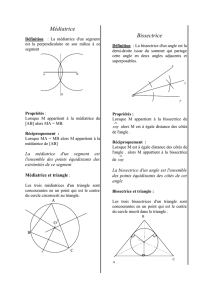
Soit ABC un triangle quelconque.
DE la médiatrice de BC, coupe la bissectrice de l’angle A en E. (Remarque : E se trouve sur le cercle circonscrit au triangle).
H et K sont les projections orthogonales de E sur [AB] et [AC].
comme E est sur la médiatrice de [BC] : EB=EC (ensemble des points équidistants des extrémités du segment)
comme E est sur la bissectrice de l’angle A : EH=EK (ensemble des points équidistants des côtés de l’angle)
les deux triangles rectangles BEH et CEK sont donc isométriques
on en déduit l’égalité de leurs troisièmes côtés : BH = CK (on peut aussi utiliser Pythagore pour le démontrer)
[AE] étant bissectrice de l’angle A, les angles EAH et EAK sont égaux
comme les triangles EAH et EAK sont rectangles les angles (complémentaires des précédents) HEA et KEA sont
aussi égaux
les deux triangles EAH et EAK ont deux cotés de même longueur (AE=AE) compris entre deux angles
respectivement égaux : ces deux triangles sont isométriques
on en déduit l’égalité de leurs troisièmes côtés : HA = KA
en additionnant membre à membre les deux égalités trouvées BH=CK et HA=KA on obtient : BA = CA
le triangle ABC quelconque possède donc deux côtés de même longueur
c’est à dire que tout triangle quelconque est forcément isocèle !!!
On pourrait recommencer cette démonstration en prenant B comme sommet, on en déduirait : AB= BC.
Donc un triangle quelconque est forcément équilatéral !!!
1) Alors que tous les théorèmes employés sont corrects, cette démonstration est bien sûr forcément
fausse… Elle ne peut être incorrecte qu’à un seul endroit, lequel ?
2) Un Professeur décide de construire cette figure en utilisant un logiciel de géométrie dynamique
disponible gratuitement sur internet
(exemple : Geonext http://geonext.uni-bayreuth.de/index.php?id=2453)
Donner un programme de construction utilisant les ordres contenus dans la liste ci-dessous :
« tracer le milieu de 2 points, tracer l’intersection de 2 droites, tracer un segment joignant 2 points,
placer un point et le nommer, tracer la bissectrice d’un angle,
tracer la perpendiculaire à une droite passant par un point,
tracer la projection orthogonale d’un point sur une droite, renommer un point »
(Le mieux serait que vous téléchargiez ce logiciel, et que vous vous entraîniez à le manipuler.
De nombreuses explications sont disponibles.)
3) Comment ses élèves vont-ils mettre en évidence l’erreur contenue dans la démonstration ci-dessus ?
4) Quel est l’intérêt de ce genre de logiciel ?
H
K
A

Paradoxe
1) Le seul point qui pose problème est :
« en additionnant membre à membre les deux égalités trouvées BH=CK et HA=KA on obtient : BA = CA »
Pour pouvoir affirmer cela il faut admettre que H et K sont situés entre les extrémités des segments [BA] et
[CA]. Mais on ne l’a pas démontré ! En fait la figure est fausse …
A contrario le fait qu’il est évident que si on construit un triangle de côté 6, 10, 13 cm il ne peut être équilatéral,
cela démontre que H et K ne sont pas situés tous les deux entre les extrémités des segments [BA] et [CA].
Si H est entre A et B, nécessairement K est à l’extérieur ! Et vice versa !!!
2) Voici un exemple de programme : (à tout moment la commande « déplacer » vous permet de réduire la taille du triangle).
point A (dans géonext le A apparaît automatiquement, dans d’autres : le placer, puis le nommer) point B point C
segment A B segment B C segment A C
bissectrice B A C
milieu B C  D perpendiculaire (BC) D
intersection médiatrice et bissectrice  E
projection orthogonale E sur (AB) renommer F  H (si comme dans géonext l’appellation F est automatique)
projection orthogonale E sur (AC) renommer F  H (si comme dans géonext l’appellation F est automatique)
segment B H segment K C
3) En utilisant la commande « déplacer » les élèves peuvent faire varier la position de B et s’apercevoir que si H
est entre A et B, nécessairement K est à l’extérieur ! Et vice versa !!! Ce n’est pas une « démonstration », c’est
une conjecture basée sur une observation de nombreuses figures (c’est plus une démarche scientifique, que
mathématique). Ils remarqueront une position « limite » : lorsque H est confondu avec B, K est confondu avec C.
Ensuite si H « part » d’un côté, K « part » de l’autre !

Ils pourront également construire le cercle circonscrit (dans géonext c’est une commande) et voir qu’il passe
bien par E.
4) Ici l’intérêt est, en déformant la figure, d’avoir très rapidement une multitude d’exemples qu’il serait bien sûr
impossible de construire à la main. Cela permet d’émettre des conjectures qui peuvent ensuite faire l’objet (ou
non selon la difficulté) d’une véritable démonstration.
Ils permettent également la réalisation de figures très précises évitant les maladresses dans l’utilisation de vrais
outils. (Même si bien sûr de véritables constructions doivent être réalisées parallèlement à l’utilisation de ces
logiciels).