Loupe et microscope (principe)

TB3 / Travaux pratiques de physique / Bachard Eric / 08/95
page 1 / 6
Loupe et microscope (principe)
Travail préliminaire : lire tout le texte et préparer (avant la séance de TP) les
questions numérotées. Cette préparation devra apparaître dans le compte
rendu, rendu obligatoirement en fin de séance.
1 La loupe
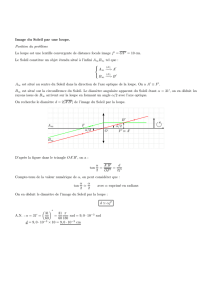
Introduction : l'oeil est un système convergent, qui ne peut voir que des objets réels et des
images virtuelles (oeil "normal").
Pour information, voir la planche “ défauts de l’oeil ” affichée en salle de TP.
But : on veut utiliser un instrument qui va donner d'un petit objet réel une image virtuelle
agrandie : la loupe.
Q1 : montrer que ceci n'est possible qu'avec un système optique convergent, dont on
précisera les conditions d'utilisation.
Remarque : on supposera que le système est une lentille mince.
1.1) Généralités
Une loupe est un système convergent, assimilable à une lentille mince, de faible distance
focale (une dizaine de cm). On l'utilise pour observer de petits objets, difficiles à observer à
l'oeil nu sans fatigue. L'objet est placé entre le plan focal objet et la lentille. L'image ainsi
obtenue est donc virtuelle, droite et agrandie : l'oeil peut l'observer.
Exemple : une personne âgée utilise une loupe pour lire le texte d'un journal.
Définitions importantes :
Puissance : soit AB la taille de l'objet et ' l'angle sous lequel on observe son image, donnée
par la loupe (voir figure 1, page suivante). La puissance P d'une loupe est le rapport
PAB
.
Avec P en dioptries (ou
m1
), ' en rad. et AB en m.
On appelle puissance intrinsèque, notée
Pi   Df
1
, la valeur de P obtenue dans les deux cas
particuliers suivants :
-L'objet est dans le plan focal objet [ F ]. L'image A'B' est à l'infini, et vue sans
accommodation par un oeil normal (emmétrope). ' est alors indépendant de la position de
l'oeil. Toutefois, en pratique, on place l'oeil près de la loupe de manière à augmenter le champ

TB3 / Travaux pratiques de physique / Bachard Eric / 08/95
page 2 / 6
visuel.

TB3 / Travaux pratiques de physique / Bachard Eric / 08/95
page 3 / 6
-L'oeil est placé dans le plan focal image [ F' ]. L'image se forme entre le point proche et le
point éloigné de l'oeil et est vue en accommodant plus ou moins. Elle est plus ou moins
grande, mais son diamètre apparent ' est invariable.
En dehors de ces deux cas particuliers, P dépend de f ', de la position de l'objet et de la
position de l'oeil. En pratique, on s'approche toujours beaucoup de P Pi.
Grossissement : A l'oeil nu, il faut placer l'objet au point proche, c’est à dire à d m pour
l'observer dans les meilleures conditions possibles. On appelle m le diamètre apparent
correspondant.
Grâce à la loupe, on peut observer l'image, qui semble placée à d m , sous l'angle ' > m .
C'est là l'intérêt de l'instrument. On appelle grossissement le rapport
G
m
'
. On voit aussi
(voir figure 2, ci-dessous ) que
'
m
est aussi égal au rapport
ii'
des images rétiniennes.
Figure 2 :
Q2 : montrer que G = P. dm , avec dm : distance du point proche à l'oeil.
Par convention, on prend dm = 25 cm =
1
4m
. Dans ce cas, l'image est rejetée à l'infini, et G
devient Gc =
Pi
4
. Gc est appelé grossissement commercial de la loupe.

TB3 / Travaux pratiques de physique / Bachard Eric / 08/95
page 4 / 6
1.2) Manipulations
Mesure du grossissement à l'aide d'une chambre claire
1.2.1) Principe
L'idée consiste à superposer deux images virtuelles (voir figure 3), toutes deux placées à la
distance dm = 25 cm. Une des deux images est une règle en vraie grandeur, l'autre est l'image
agrandie de l'objet dont on connaît les dimensions. Il suffira de lire les dimensions de l'image
agrandie pour arriver à G et P, car dans les conditions d'observation, on a :
GA B
AB
m
On appellera chambre claire le dispositif qui permet de réaliser cette superposition.
Q3 : démontrer que G = , dans les conditions décrites.
On prendra le quadrillage
d'un papier millimétré
pour objet AB (AB = 1
mm, par exemple).
La mesure de A'B' est
donnée par la règle.
1.2.2) Schéma du montage : il est donné figure 4, ci dessous :
O désigne le centre de l'oeil de l'observateur. La loupe
(L) est symbolisée par la lentille mince convergente.
(Lm) désigne la lame mince qui fait office de chambre
claire.

TB3 / Travaux pratiques de physique / Bachard Eric / 08/95
page 5 / 6
Q4 : montrer que M'N' est bien l'image de la règle donnée par la lame. Quel dispositif
connu donnerait la même image ?
Remarque : le dispositif chambre claire peut désigner indifféremment une lame transparente
mince, une lame semi-réfléchissante ou un prisme de Govi (qui correspond à une lame semi-
réfléchissante épaisse).
Exemple : un miroir plan dont le tain a été enlevé peut constituer un excellente chambre
claire.
La difficulté de cette manipulation va donc consister à placer l'image de la règle exactement à
la distance dm de l'oeil.
1.2.3) Mode opératoire
On utilise un banc d'optique portant le quadrillage objet, la loupe munie de la chambre claire,
un oeilleton (destiné à maintenir l'oeil dans une position fixe).
La règle est placée horizontalement sur un support, à hauteur de l'axe de la loupe, et
parallèlement à cet axe.
1) Mesurer, par une méthode simple (autocollimation, par exemple) la distance focale f ' de la
lentille mince servant de loupe.
2) Positionner la loupe sur le banc. Et placer la règle MN à 25 cm de l'oeil. Pour cela, on
placera l'oeilleton à f '-15 mm derrière la loupe, et on admettra que le centre optique O de
l'oeil se trouve à 15 mm derrière l'oeilleton. O et F' seront ainsi confondus.
4) Pour placer la règle MN à 25 cm de O :
-mesurer O ( désigne le centre de la lame, placé sur l'axe principal optique)
-placer la règle à 25 cm - O de l'axe, parallèlement à l'axe.
5) Rapprocher l'objet de la loupe (ce qui rapproche l'image) jusqu'à supprimer la parallaxe,
c'est à dire jusqu'à ce que A'B' et M'N' (image de MN par la lame) soient confondues.
6) Mesurer alors , égal à G dans ces conditions.
1.2.4) Exploitation des résultats de mesure
Montrer que G mesuré est égal à Gc.
Estimer les incertitudes de mesure. Conclusions ?