cours distances

4
ème
cours distances
1
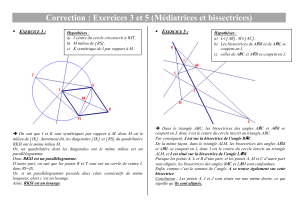
1 Distance d’un point à une droite
Soit un point A qui n’appartient pas à (d). Le point de (d) le plus proche de A est le
point H tel que la droite (AH) est perpendiculaire à (d).
AH est appelée la distance du point A à la droite (d)
Pour tout point M de (d) non confondu avec H, on a AH < AM.
Démonstration :
Soit A’le symétrique de A par rapport à la droite (d).
La droite (AA’) coupe (d) en H.
En utilisant l’inégalité triangulaire dans le triangle AMA’, on peut écrire :
AA’ < AM + A’M
Or AA’ = 2xAH (car H est le milieu de [AA’]) et AM = A’M (car (d) est la médiatrice
de [AA’])
Donc 2 xAH < 2 x AM
Soit AH < AM
A
A’
H
M (d)

4
ème
cours distances
2
2 Position relative d’une droite et d’un cercle
La droite est sécante au cercle
 deux points en commun
 OH < rayon
La droite est tangente au cercle
 un seul point en commun
 OH = rayon
 La droite (d) est perpendiculaire au rayon [OH].
La droite est extérieure au cercle
 aucun point en commun
 OH > rayon
O
H
(d)
O
H
(d)
O
H
(d)

4
ème
cours distances
3
3 Bissectrice d’un angle et équidistance
Propriété 1 : Si un point appartient à la bissectrice d’un angle, alors il est équidistant
des côtés de cet angle.
Propriété 2 : Si un point situé entre les côtés d’un angle saillant est équidistant des
côtés de l’angle, alors il appartient à la bissectrice de cet angle.
M appartient à la bissectrice de l’anglea xOy. MH = MK
4 Bissectrices d’un triangle et cercle inscrit
Les bissectrices d’un triangle sont les bissectrices de chacun des angles du triangle.
Propriété 1 : Les trois bissectrices d’un triangle sont concourantes.
Propriété 2 : Le point de concours des trois bissectrices d’un triangle est le centre
d’un cercle tangent aux trois côtés de ce triangle.
Ce cercle est appelé le cercle inscrit dans le triangle.
Les bissectrices du triangle ABC sont
concourantes en I.
I est équidistant des trois côtés du
triangle ABC : IH = IK = IL.
Le cercle inscrit dans le triangle ABC
a pour centre I et pour rayon IH.
Remarque :
Pour construire le centre du cercle inscrit dans un triangle, il suffit de tracer les
bissectrices de deux angles du triangle.
Propriété 1
Propriété 2