Constructions à la règle et au compas - Christian Côté

Constructions à
la règle et
au compas
Christian Côté
Cégep de Terrebonne

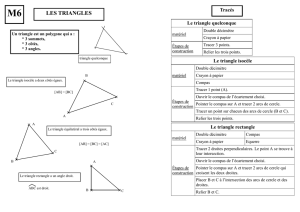
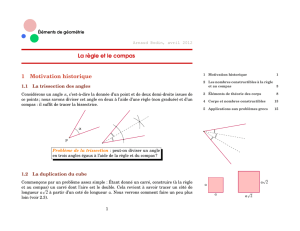
1. Quadrature du cercle
Peut-on construire, à la règle et au compas, un carré
ayant la même aire qu’un cercle donné?
r

1. Quadrature du cercle
Peut-on construire, à la règle et au compas, un carré
ayant la même aire qu’un cercle donné?
r

2. Duplication du cube
Peut-on construire, à la règle et au compas, un cube
ayant le double du volume d’un cube donné?
Volume =
Volume =
L
3
L
3
2L
L
32

3. Trisection de l’angle
Peut-on séparer, à l’aide d’une règle et d’un
compas, un angle donné en trois parties égales?
A
O B
C
D
Angle AOC = Angle COD = Angle DOB