MODÉLISATION Quelques aspects du vol d`un avion PRESENTATION

Spé ψ
ψψ
ψ 2015-2016 page 1/16 Devoir n°4
Spé ψ
ψψ
ψ 2015-2016 Devoir n°4
MODÉLISATION
Quelques aspects du vol d’un avion
L'Airbus A380 est un avion de ligne civil gros-porteur long-courrier quadriréacteur à double
pont produit par Airbus, filiale d'EADS, construit principalement en Allemagne, Espagne, France et
Royaume-Uni et assemblé à Toulouse.
Gros-porteur très long-courrier, ce quadriréacteur symbolise l'aboutissement de la politique
de gamme menée par le constructeur européen depuis la commercialisation de son premier avion,
l'A300.
Spécifications A340-500 A340-600 A380
Longueur hors-tout (en m) 67,90 75,30 73
Envergure (en m) 63,45 63,45 79,8
Surface alaire (en m
2
) 437 437 845
Capacité en sièges 313 378 525
Autonomie (en km et en Nm) 15800/8.500 13900/7.500 15400/8280
Poids au décollage (en t) 368 369 492
Capacité des réservoirs (en L) 214800 194880 256600
Moteurs 4 Trent 553 4 Trent 556 4 Trent 900
Poussée d’un réacteur (en kN) 236 249 310
L’énoncé comporte plusieurs parties indépendantes :
PRESENTATION
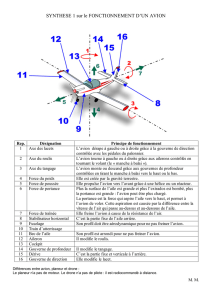
1-Les commandes de vol primaires
Pour piloter un avion, il est nécessaire de pouvoir contrôler en permanence ses évolutions
dans l’espace suivant trois directions ou axes (voir Figure 1 page 2) :
 l'axe de lacet (vertical) ;
 l'axe de roulis (horizontal et dans la direction de la marche) ;
 l'axe de tangage (horizontal et perpendiculaire à la marche).
Pour cela, le pilote agit sur les commandes de vol de l’avion. En pratique, on distingue deux
types de commandes :

Spé ψ
ψψ
ψ 2015-2016 page 2/16 Devoir n°4
 les commandes de vol primaires utilisées pendant tout le vol qui permettent de contrôler
l’évolution de l’avion autour de ses axes de référence :
 la gouverne de direction ou gouvernail pour le lacet,
 les ailerons et les spoilers pour le roulis,
 les gouvernes de profondeur et le plan horizontal réglable (PHR) pour le tangage.
 Les commandes de vol secondaires utilisées pendant les phases d’atterrissage et de décol-
lage qui permettent de modifier la configuration aérodynamique de l’avion :
 hypersustentateurs (volets et becs) pour la portance ;
 les spoilers (ou aérofreins) pour la traînée.
Figure 1 : Les commandes de vol de l’A380
2- Les gouvernes de profondeur
L’Airbus A 380 est équipé de quatre gouvernes de profondeur disposées symétriquement sur
le plan horizontal réglable (PHR) de l’avion (voir Figure 2 ).
Gouverne Extérieure Droite (ED)
Gouverne Intérieure Droite (ID)
Gouverne Intérieure Gauche (IG)
Gouverne Extérieure Gauche (EG)
PHR
Figure 2
: Les gouvernes de profondeur

Spé ψ
ψψ
ψ 2015-2016 page 3/16 Devoir n°4
Chaque gouverne de profondeur est reliée au PHR par des charnières ou liaisons pivots (voir
Figure 3) et est mue en rotation par une unité de commande constituée de deux actionneurs :
 une servocommande (SC), actionneur principal relié au circuit hydraulique de
l’avion
 un EHA (Electro Hydraulic Actuator : actionneur électro-hydrostatique), utilisé en
cas de défaillance de la servocommande ou du circuit hydraulique principal. Cet actionneur est ali-
menté électriquement et produit localement, via un moteur électrique entraînant une pompe,
l’énergie hydraulique nécessaire à son fonctionnement
Ces unités de commande sont identiques pour les quatre gouvernes de profondeur.
3-Les repères et paramètres angulaires associés à l’avion
Afin d’étudier le comportement de l’avion, on définit (voir figure 4) les repères R
0
, R
A
, et R
B
passant par le point G, centre de gravité de l’avion ainsi que les repères R
P
et R
C
passant par le point
B, centre de poussée du PHR et des gouvernes de profondeur :
(
)
0
0
0 0
, , ,
R G x y z
= repère animé d’un mouvement de translation par rapport au galiléen où
0
z
est la verticale descendante du lieu ;
(
)
, , ,
A
A
A A
R G x y z
= repère aérodynamique tel que la vitesse de l’avion soit
(
)
A
V V t x
= ;
(
)
, , ,
B
B
B B
R G x y z
= repère lié à l’avion avec
(
)
,
b
G x
axe longitudinal de l’avion ; ;
(
)
, , ,
P
P
P P
R G x y z
= repère lié au PHR avec
(
)
,
P
B x
axe de symétrie longitudinal ; ;
(
)
, , ,
C
C
C C
R G x y z
= repère lié aux gouvernes avec
(
)
,
C
B x
axe de symétrie longitudinal .
Remarque : attention pour la suite du sujet au sens de z utilisé en aéronautique.
La mise en place de ces repères permet de définir, dans le cas d’un vol symétrique, c'est-à-
dire dans le cas où les plans
(
)
0
0
, ,
G x z
et
(
)
, ,
B
B
G x z
sont confondus, les paramètres de position
angulaire suivants (voir Figure 4) :
 l’assiette longitudinale ou angle θ entre l’horizontale
0
x
et l’axe
B
x
de l’avion :
Unité de commande de
la gouverne intérieure
gauche (IG)
Charnière
Unité de commande de
la gouverne extérieure
gauche (EG)
Gouverne
Actions
aérodynamiques
Charnières
Unité de
commande
PHR
Figure 3 : Unités de commande des gouvernes gauches

Spé ψ
ψψ
ψ 2015-2016 page 4/16 Devoir n°4
 quand θ augmente, on dit que l’avion se cabre,
 quand θ diminue, on dit que l’avion pique ;
 la pente γ ou angle entre l’horizontale
0
x
et le vecteur vitesse
(
)
A
V V t x
= de l’avion ;
 l’incidence α ou angle
(
)
,
A B
x x
.
On note d’autre part
 δ : inclinaison du PHR par rapport à l’avion ou angle
(
)
,
B P
x x
;
 β : inclinaison des gouvernes par rapport au PHR ou angle
(
)
,
P C
x x
.
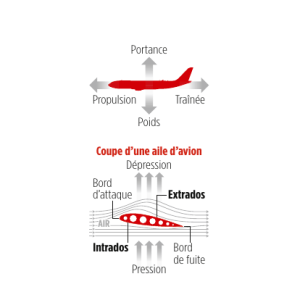
4-Les forces appliquées à l’avion
Les forces appliquées à l’avion sont, entre autres :
 le poids de l’avion agissant suivant
(
)
0
,
G z
:
0
P mg z
= où m est la masse de l’avion chargé ;
 la force de poussée des réacteurs agissant suivant
(
)
,
B
G x
R
B
F F x
= .
 les forces de portance et de traînée appliquées au centre de poussée des surfaces portantes
portance
A
P P P z
= = − avec P > 0 si α ≥ 0 ;
traînée
A
T T T x
= = − avec T > 0.
On établit que :
2
1
2
z
P v C A
= ρ et 2
1
2
x
T v C A
= ρ .
ρ désigne la masse volumique du fluide
A est l’aire des surfaces portantes
C
z
est le coefficient de portance ;
C
x
est le coefficient de traînée ou résistance à l’avancement.
x
0
z
0
x
A
z
A
x
B
z
B
G
θ
γ
α
F
PA
F
TA
F
R
P
F
PP
A
B
V
z
A
x
c
F
PG
β
x
P
δ
Figure 4 : Repères associés à l’avion
α
: incidence
γ : pente
θ : assiette
θ = α + γ
Horizontale
Aéronautique
Avion

Spé ψ
ψψ
ψ 2015-2016 page 5/16 Devoir n°4
A PARTIR DE CE POINT REDIGER LE DS SUR LA COPIE DE PHYSIQUE
PARTIE I :
É TUDE DE L ’ ATMOSPHERE ET DE CERTAINS INSTRUMENTS DE VOL
Étude de l’atmosphère
On assimile l’air à un gaz parfait, dont la masse molaire est M = 29 g⋅mol
–1
et le rapport des
capacités thermiques massiques
P
V
c
c
γ =
= 1,4 . La masse volumique est notée ρ . Le champ de pe-
santeur est supposé uniforme
z
g g u
= − où
z
u
est un vecteur unitaire selon la verticale ascendante
du lieu, et g = 9,8 m ⋅ s
–2
.
La constante des gaz parfaits est R = 8,31 J ⋅ K
–1
⋅ mol
–1
.
Question I-1 : On commence par utiliser un modèle d’atmosphère isotherme, dont la tempé-
rature T
0
= 298 K est uniforme et constante dans le temps.
a) Quelle est l’équation locale de la statique des fluides dans le cadre de cette étude ?
b) Comment s’exprime la masse volumique ρ en fonction notamment de la pression
et de la température ?
c) En déduire l’expression de la pression P en fonction notamment de l’altitude z , en
posant P = P
0
pour z = 0. Faire apparaître une constante H homogène à une distance. On prendra
pour la suite P
0
= 1,0 bar.
d) Exprimer la masse volumique ρ de l’air en fonction notamment de l’altitude z, en
posant ρ = ρ
0
pour z = 0.
e) Application numérique : calculer la masse volumique de l’air pour z = 0 et pour
z = 13 km.
f) En aéronautique de loisir, on a l’habitude de dire que la pression chute de 1 hPa
tous les 28 ft (pieds). On rappelle que 1 ft = 0,30 m. Montrer que cette règle pratique est cohérente
avec le résultat précédent pour les faibles altitudes.
g) Quel instrument de vol exploite la relation P ( z ) ?
Question I-2 : En réalité, la température diminue lorsque l’altitude augmente. On adopte un
modèle affine, la température diminuant de 0,65°C à chaque fois que l’altitude augmente de 100 m.
On prend T = T
0
= 288 K pour z = 0.
a) On pose
(
)
(
)
0
1
T z T z
= − α
. Donner la valeur numérique de α .
b) En aéronautique, on utilise l’atmosphère « normalisée » ISA (International Stan-
dard Atmosphere), qui tient compte de valeurs moyennes sur le globe terrestre à la latitude 45° nord
(tableau ci-dessous). Les valeurs du tableau sont-elles en accord avec le modèle affine de la ques-
tion a) ?
Altitude (m) 0 500 1000 1500 2000 2500 3000
Pression (hPa) 1013 955 900 845 794 746 700
Température (°C) 15,0 12,0 8,5 5,5 2,0 –1,0 –4,5
Altitude (m) 3500 4000 5000 6000 7000 8000 9000
Pression (hPa) 658 617 541 471 411 357 307
Température (°C) –7,5 –11,0 –17,5 –24,0 –30,5 –37,0 –43,5
c) On souhaite connaître le gradient de pression
dP
dz
pour les différentes valeurs de z
du tableau. Expliquer comment estimer simplement ces valeurs, de façon approchée.