DACB - La Botte Des MATHS

G 4/7
P ARALLÉLOGRAMME 5ième
I. D EFINITION DU PARALLÉLOGRAMME .
Un parallélogramme est un quadrilatère dont les côtés opposés sont parallèles.
(AB) // (CD)
et
(AD) // (BC)
II. C ENTRE DE SYMÉTRIE D ’ UN PARALLÉLOGRAMME .
Dans un parallélogramme, le point d’intersection O des diagonales est un centre de symétrie. On dit
parfois que ABCD est un parallélogramme de centre O.
Conséquences :
1. Dans un parallélogramme, les diagonales se coupent en leur milieu.
c’est à dire : Les diagonales [AC] et [BD] ont le même milieu O.
2. Dans un parallélogramme, les cotés opposés sont égaux 2 à 2.
c’est à dire : AB = CD et AD = BC.
3. Dans un parallélogramme, les angles opposés sont égaux 2 à 2.
c’est à dire : a ABC= a CDAErreur ! Signet non défini. et a
aa
a
DAB = a BCD.
III. C OMMENT DÉMONTRER QU ’ UN QUADRILATERE EST UN PARALLÉLOGRAMME ?
a. Caractérisation d’un parallélogramme par sa définition.
S I un quadrilatère a ses côtés 2 à 2 parallèles, A LORS ce quadrilatère est un parallélogramme.
b. Caractérisation d’un parallélogramme par ses diagonales.
S I les diagonales d’un quadrilatère ont le même milieu, A LORS ce quadrilatère est un
parallélogramme.
A
B
D
C
O
D
A
C
B

G 4/7
P ARALLÉLOGRAMME 5ième
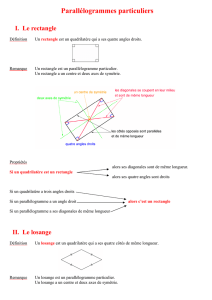
IV.L E RECTANGLE :
Propriétés :
- Le rectangle est un parallélogramme particulier donc il en a
toutes les propriétés.
- Les diagonales du rectangle ont même milieu et même
longueur.
Comment démontrer qu’un quadrilatère est un rectangle ?
 Si un quadrilatère a 3 angles droits alors c’est un rectangle.
 Si un quadrilatère a ses diagonales de même longueur et qui se coupent en leur milieu
alors c’est un rectangle.
Comment démontrer qu’un parallélogramme est un rectangle ?
 Si un parallélogramme a un angle droit alors c’est un rectangle.
 Si un parallélogramme a ses diagonales de même longueur alors c’est un rectangle.
II.L E LOSANGE
Propriétés :
- Le losange est un parallélogramme particulier donc il
en a toutes les propriétés.
- Les diagonales du losange ont même milieu et sont
perpendiculaires.
Comment démontrer qu’un quadrilatère est un
losange ?
 Si un quadrilatère a ses 4 côtés de même longueur
alors c’est un losange.
 Si un quadrilatère a ses diagonales perpendiculaires et qui se coupent en leur milieu
alors c’est un losange
Comment démontrer qu’un parallélogramme est un losange ?
 Si un parallélogramme a 2 côtés consécutifs de même longueur alors c’est un losange.
 Si un parallélogramme a ses diagonales perpendiculaires alors c’est un losange.
D
A
C
B
D
C
B
A

G 4/7
P ARALLÉLOGRAMME 5ième
III. L E CARRÉ :
D
A
C
B
Propriétés :
- Le carré est un parallélogramme particulier donc il en a toutes les propriétés.
- Le carré est un losange particulier donc il en a toutes les propriétés.
- Le carré est un rectangle particulier donc il en a toutes les propriétés.
- Les diagonales du carré ont même milieu, même longueur et sont perpendiculaires.
Comment démontrer qu’un quadrilatère est un carré ?
 Si un quadrilatère est à la fois un losange et un rectangle alors c’est un carré.
 Si un quadrilatère a ses diagonales perpendiculaires, de même longueur et qui se coupent en leur milieu
alors c’est un carré.
Comment démontrer qu’un parallélogramme est un carré ?
 Si un parallélogramme a 2 côtés consécutifs de même longueur et un angle droit alors c’est un carré.
 Si un parallélogramme a ses diagonales perpendiculaires et de même longueur alors c’est un carré.