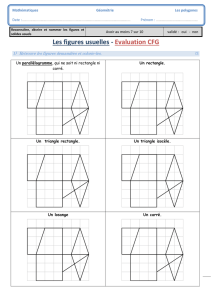
La planche à clous

1
. . . . .
. . . . .
. . . . .
. . . . .
. . . . . La planche à clous
Si la dénomination de planche à clous donne une image instantanée de l’outil,
l’appellation géoplan en éclaire davantage l’utilisation didactique.
Le géoplan est une planche sur laquelle s’organisent des réseaux de clous, entre lesquels
seront tendus des élastiques permettant de construire divers «!objets!» de géométrie plane!:
des segments de droite (portions de droites) obtenus en joignant des clous alignés,
des triangles en joignant trois clous non alignés, des contours polygonaux concaves ou non,
diverses figures géométriques.
• Construction d’un géoplan
A l’école primaire, on utilise essentiellement deux types de géoplans!:
- le géoplan à quadrillage, construit à partir de deux réseaux de clous de directions
perpendiculaires,
- le géoplan circulaire, moins utilisé, permettant d’approcher le cercle à partir
de clous, sommets de contours polygonaux au nombre de côtés croissant.
Parmi ceux-ci, le géoplan circulaire à 12 clous, sommets d’un dodécagone,
permet de travailler l’heure et ses subdivisions.
Le géoplan à quadrillage se construit à l’aide d’un gabarit en papier, sur lequel
est tracé un maillage de lignes et de rangées de directions perpendiculaires.
Posé sur une planche de bois carrée dont les dimensions varient entre 30cm et 50cm de côté,
il permet de planter les clous avec précision et sans laisser aucune trace de repère sur le
géoplan .
En fonction de la taille de la planche, les clous distants de 2cm à 4cm ne dépasseront pas de la
planche de plus de 5mm à 7mm (il est préférable de choisir des clous sans tête, pour éviter de
s’y griffer les doigts). Le choix d’un bois de type «!aggloméré!» évitera d’avoir
à manipuler une planche trop lourde.
Le choix de placer un nombre impair de clous par ligne, permettra d’en pointer
le «!clou milieu!».
Les clous périphériques seront distants d’au moins 5cm du bord de la planche.
La planche pourra, si on le désire, garder la couleur naturelle du bois!; un fond rouge ou
lumineux et toujours monochrome rendra la lisibilité optimale.
Aucun artifice de décoration ne sera ajouté.
Pour certains bois, il est utile de poncer les bords de la planche pour en éliminer les
irrégularités

2
Une quantité importante d’élastiques de couleur et de longueur différentes sera mise à
disposition des élèves.
Un géoplan peut facilement être construit par les enfants eux-mêmes; le choix se portera sur
un support carré constitué d’une couche de frigolite recouverte d’une couche de liège, le tout
planté « de punaises de signalisation!».
• Qualités didactiques de l’outil
Cet outil conçu par Caleb Gattegno est un excellent matériel d’exploration dynamique,
autorisant essais et erreurs successifs, encourageant la créativité, invitant à la recherche,
premiers pas d’un apprentissage constructiviste.
Caleb Gattegno est un mathématicien d’origine égyptienne, ayant mené d’importants travaux en didactique des
mathématiques!: la consultation des sites qui lui sont consacrés ne manque pas d’intérêt
• Utilisation du géoplan
Le géoplan peut-être utilisé dès l’âge de 5 ou 6 ans, et ce, jusqu’au collège!; il sera utile d’y
revenir régulièrement lors des cours de géométrie, comme support visuel ou outil de
recherche.
Avant toute activité, les enfants observeront la planche qui leur est présentée, pour en
découvrir, de manière intuitive d’abord, de manière plus précise par la suite, le principe de
construction tout en traduisant par des mots mathématiques l’organisation du quadrillage.
Les notions «!d’espace clous!» (espace entre deux clous consécutifs) et «!de carré clous!»
(carré minimal limité par 4 clous disposés en carré), seront importantes pour la reproduction
sur papier pointé (une feuille A4, reproduisant partiellement les maillages du géoplan).
1. Premières activités sur le géoplan!
• Créations libres figuratives ou non (3e maternelle/grande section, 1re primaire/CP).
• Reconstructions, par les enfants, de figures imposées sur le!«!grand géoplan du
maître!» avec respect de l’échelle (espaces clous).
• Constructions de dessins à thème imposé, de figures géométriques (nommées).
Activités de spatialisation (dictée spatiale, trajets de type logo*, …) sur la planche
déposée sur la table!: création d’un repère à l’aide d’une perle ou d’une gommette
posée sur un clou arbitraire (central ou inférieur gauche). Cette spatialisation peut être
retravaillée en redressant la planche!: le passage du plan horizontal au plan vertical se
faisant naturellement.
* n pas en avant, m pas à droite….

3
• Identification dans certaines créations de figures géométriques usuelles
(carré, rectangle, triangle, …, contours polygonaux divers).
• Mise en évidence de figures convexes (et non convexes), conduisant à la construction
de sa définition.
• Etude de figures géométriques usuelles!par aller-retour!successifs : construire des
figures, les transformer (étirer ou rétrécir les côtés, modifier leur inclinaison).
Observer les propriétés, nommer les éléments géométriques des figures (sommets,
côtés, longueur d’un côté exprimée en espaces clous).
• Tracer des figures isométriques.
Au fil des constructions, apparaîtront les notions de portion de droite ou segment, direction,
segments parallèles ou perpendiculaires. Les angles droits, aigus ou obtus prendront tout leur
sens grâce à la mobilité des côtés des angles.
2. Traces papier, reproduction à l’échelle
Les traces papier crayon certes figées, permettront néanmoins de garder une trace du travail
de l’enfant. Elles se feront sur des feuilles pointées de format A4, (avec reproduction des
bords du géoplan comme repère pour les plus jeunes).
Les reproductions se feront «!à l’identique!», espace points pour espace clous, en réalité à
l’échelle.
3. Quadrilatères et triangles
• Construction des divers quadrilatères par modifications successives des côtés
(longueurs et directions) et des amplitudes d’angles, conduisant à leur classement
( quelconque, trapèze, parallélogramme, losange, rectangle, carré).
• Construction et observation des propriétés des diagonales et médianes des
quadrilatères usuels.
• Droites remarquables!: médiatrice d’un segment, hauteur d’un parallélogramme ou
d’un triangle.
• Etude des familles de triangles (seul le triangle équilatéral ne peut-être construit sur
géoplan).
• Construction de figures semblables.

4
4. Périmètre des polygones
Les élastiques,!«!en soi!», ne permettront bien évidemment pas de mesurer le contour
d’une figure!; dans tous les cas, une ficelle contournant le polygone donnera sens au
concept de périmètre.
Pour les carré et rectangle dont les côtés sont placés sur le maillage du géoplan,
l’identification des côtés, ou des longueur et largeur, permettra de déterminer la
mesure du périmètre exprimée en étalon espace clous.
En pointant sur la ficelle, les sommets de la figure par des traits de couleur, et en
identifiant les objets géométriques tels que longueur, largeur, hauteur…, la formule
générale du périmètre des figures usuelles sera construite sans peine.
5. Aire des polygones
Sur le géoplan, le carré clous servira d’étalon pour exprimer la mesure du
recouvrement ou aire d’une figure.
Pour les figures dont les côtés ne reposent pas sur le maillage, l’aire s’exprimera par
un encadrement (minimum et maximum) de carrés clous.
Les caractéristiques du géoplan permettent de donner sens à la construction
des formules d’aires des carré et rectangle, en partant de figures dont les côtés
reposent sur les deux directions de la planche à clous.
Dans le cas du rectangle, la formule d’aire sera donnée par le produit du nombre
obtenu par comptage des carrés clous «!rangés!» le long de la longueur, par le nombre
de rangées contenues dans la largeur, le tout exprimé en carrés clous.
Quantité d’autres figures pouvant être obtenues par déformation ou déconstruction du
rectangle, leurs formules d’aire s’établiront automatiquement.
6. Transformation du plan et de ses figures
La symétrie axiale!
L’utilisation d’un miroir, ou mieux encore du géomiroir *placé le long d’une des
directions du maillage, permettra de reconstruire l’image d’une figure donnée par
rapport à l’axe de symétrie que constitue le bord du miroir.
Grâce à l’observation des positions relatives des deux figures, de leur isométrie, on
énoncera la définition de la symétrie axiale, dite aussi orthogonale.
Dans les figures étudiées antérieurement, certaines droites remarquables peuvent
être identifiées comme axe de symétrie.

5
7. Quelques propositions supplémentaires!:
a. Vérification de la transitivité éventuelle des relations de parallélisme et de
perpendicularité de segments
b. définition de la taxi-distance ou distance de Manhattan
c. construction d’un repère cartésien et définition des coordonnées cartésiennes
d’un point (exprimées en espaces clous)
d. introduction au théorème de Thalès
e. définition de la notion de vecteur, et par application, d’une translation
f. première approche de la trigonométrie (sur géoplan circulaire)
g. étude de la notion d’inclinaison ou de pente
h. reproductions de figures à diverses échelles
i. transformation d’une figure d’aire donnée, en une autre figure de même aire
j. transformation d’une figure (un carré, un rectangle, …), en une figure dont
l’aire vaut le double!de la première
k. pour une figure de périmètre et d’aire donnés, construire des figures
de même périmètre et vérifier si l’aire est conservée (et inversement).
Cette liste d’activités de dépassement est non exhaustive.
Seul l’usage répété de la planche à clous, permettra d’en découvrir la richesse!; l’imagination
fera le reste, l’enthousiasme des enfants finira de vous convaincre.
Renée Vanderstraeten,
maître assistante en didactique des mathématiques
département pédagogique de la Haute Ecole de Bruxelles.
[email protected]
le géoplan . . . . .
. . . . .
. . . . .
. . . . .
. . . . .