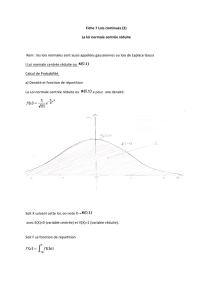
5. Comparaisons Statistiques

5. Comparaisons Statistiques
Test d'hypothèse (Neyman et Pearson)
état réalisé
!0est réalisée !1est réalisée
jugement porté !0est vraie jugement correct "1#$% jugement faux "&, erreur de 2eespèce %
!1est vraie jugement faux "$, erreur de 1ère espèce %jugement correct "1#&%
La région d'acceptation de l'hypothèse
!0
est l'intervalle tel que pour
$
donné,
&
soit minimal.
1#&
est appelé la puissance du test.
Dans le présent document on présente les tests de conformité à un standard (sur une moyenne ou une variance) et les
tests de comparaisons (de moyennes ou variances). Les valeurs testées sont calculées à partir d’un échantillon.
Comparaison de la moyenne d'une population normale (de variance connue) à une valeur donnée
!0:'('0)M#'0
*+ n,-"0, 1%
.
On calcule
u(m#'0
*+ n
. La région d’acceptation est l’intervalle
.#u$/2,u$/20
formé des quantiles
$
2
et 1-
$
2
de la loi normale
centrée réduite pour le risque
α
choisi. Si
u1.#u$/2,u$/20
, on peut rejeter l'hypothèse au risque
α
. Sinon, on ne peut pas la
rejeter.
Comparaison de la variance d'une population normale à une valeur donnée
!0:*(*02)n S2
*02(2i(1
3"Xi#M%
*02, 42"n#1%
.
On calcule
n s2
*02
. La région d’acceptation est l’intervalle
541
2,42 26
formé des quantiles
$
2
et 1-
$
2
de la loi du
42
à
"n#1%
degrés de liberté pour le risque
$
choisi. Si
n s2
*021541
2,42 26
, on peut rejeter l'hypothèse au risque
$
. Sinon, on ne peut pas la
rejeter.
Comparaison de la moyenne d'une population normale (de variance inconnue) à une valeur donnée
!0:'('0)M#'0
S+n#1,7"n#1%
.
On calcule
t(m#'0
s+n#1
. La région d’acceptation est l’intervalle
.#t$/2,t$/20
formé des quantiles
$
2
et 1-
$
2
de la loi de Student
de degré
"n#1%
pour le risque
α
choisi. Si
t1.#t$/2,t$/20
, on peut rejeter l'hypothèse au risque
α
. Sinon, on ne peut pas la
rejeter.
Test des appariements (comparaison des moyennes de deux populations appariées)
Soit
D(Y#X
,
H0:8"D%(0)D
sD+n#1,7"n#1%
.
On calcule
t(d
sD+n#1
. La région d’acceptation est l'intervalle
.#t$/2,t$/20
formé des quantiles
$
2
et 1-
$
2
de la loi de
Student de degré
"n#1%
pour le risque
α
choisi. Si
t1.#t$/2,t$/20
, on peut rejeter l'hypothèse au risque
α
. Sinon, on ne
peut pas la rejeter.
Comparaison sur échantillons des variances de 2 populations normales
!0:*12( *22( *2)n1S129"n1#1%
n2S229"n2#1%,:"n1#1, n2#1%
.
On calcule
f(n1s129"n1#1%
n2s229"n2#1%
. La région d’acceptation est l’intervalle
.f1,f20
formé des quantiles de la loi de Snedecor à
n1#1
et
n2#1
degrés de liberté pour le risque
α
choisi. Si
f1.#f1,f20
on peut rejeter l'hypothèse au risque
α
. Sinon, on ne peut
pas rejeter l'hypothèse d'égalité des variances. Dans ce dernier cas, on retient une variance commune égale à
*;2(n1S12<n2S22
n1<n2#2
.
Comparaison sur échantillons des moyennes de 2 populations normales (le test d'égalité des variances étant déjà
réalisé)
!0:'1('2(' ) M1#M2
n1S12<n2S22
n1<n2#2=1 n1<1 n2>,7"n1<n2#2%
.
On calcule
t(m1#m2
*;1
n1<1 n2
. La région d’acceptation est l’intervalle
.#t$/2,t$/20
formé des quantiles
$
2
et 1-
$
2
de la loi de
Student de degré
"n1<n2#2%
pour le risque
α
choisi. Si
t1.#t$/2,t$/20
, on peut rejeter l'hypothèse au risque
α
. Sinon, on
ne peut pas.
www.thierry-verdel.com